Интегралы таблица интегралов шпора
Таблица основных интегралов:
Основные св-ва неопределённого интеграла:


Производная неопр. интеграла равна подинтегральной функции; дифферинциал от неопр. интеграла равен подинтегр. выражению, т.е.

Неопр. интеграл от дифферинциала некоторой фун-ии равен сумме этой фун-ии и произвольной постоянной:

Постоянный множетель можно вынести из-под знака интеграла, т.е. если k=const0, то

Неопр. интеграл от алгебраической суммы 2-х фун-ий равен алгебраической сумме интегралов от этих фун-ий в отдельности, т.е.













Основные методы интегрирования:
Метод подстановки:

формула замены переменной в неопределённом интеграле.
Метод интегрирования по частям:

формула интегрирования по частям в неопределённом интеграле.
Формула Ньюто-Лейбица(для определённого интеграла):

тогда 
Замена переменной в определённом интеграле:

Интегрирование по частям в определённом интеграле:

Простейшие производные:
Основные св-ва определённого интеграла:



при 

Доверь свою работу кандидату наук!

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.
Пусть у нас есть какая-то функция f(x).
Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).
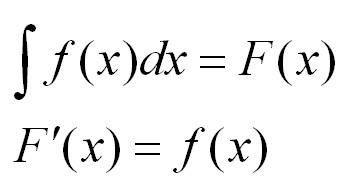
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:
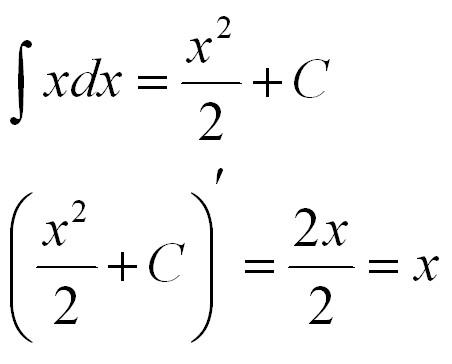
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:
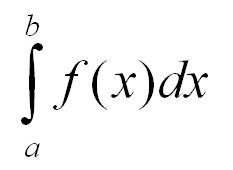
Точки а и b называются пределами интегрирования.

Бари Алибасов и группа
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правила вычисления интегралов для чайников
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
- Производная от интеграла равна подынтегральной функции:
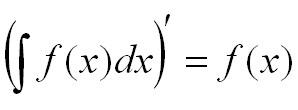
- Константу можно выносить из-под знака интеграла:
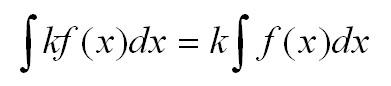
- Интеграл от суммы равен сумме интегралов. Верно также для разности:
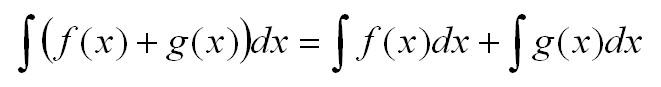
- Линейность:
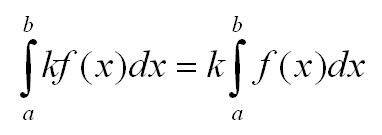
- Знак интеграла изменяется, если поменять местами пределы интегрирования:
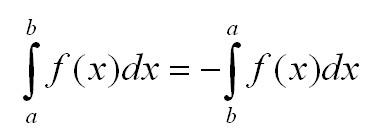
- При любых точках a, b и с:
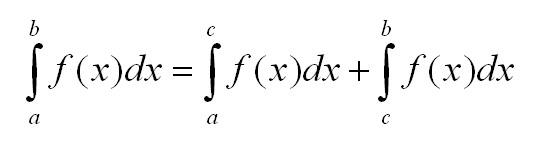
Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
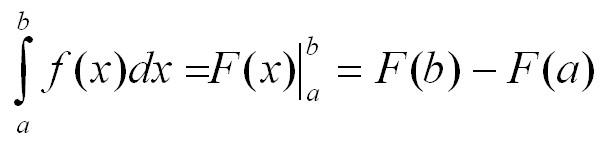
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
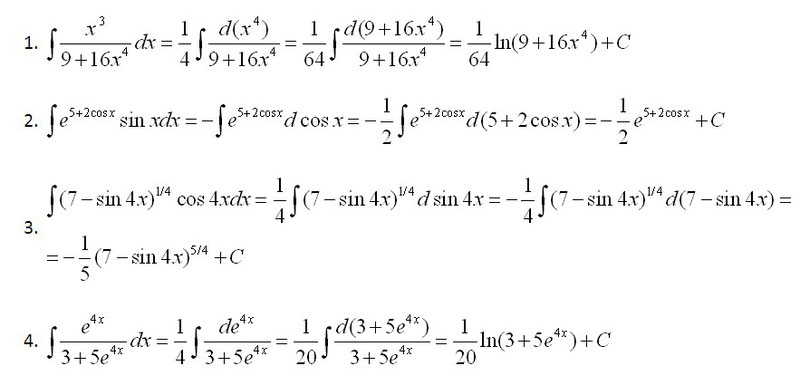
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Таблица основных неопределенных интегралов
Главные интегралы, которые должен знать каждый студент
Перечисленные интегралы - это базис, основа основ. Данные формулы, безусловно, следует запомнить. При вычислении более сложных интегралов вам придется постоянно ими пользоваться.
Обратите особое внимание на формулы (5), (7), (9), (12), (13), (17) и (19). Не забывайте при интегрировании добавлять к ответу произвольную постоянную С!
Интеграл от константы
Интегрирование степенной функции
В действительности, можно было ограничиться только формулами (5) и (7), но остальные интегралы из этой группы встречаются настолько часто, что стоит уделить им немного внимания.
∫ x d x = x 2 2 + C (2)
∫ x 2 d x = x 3 3 + C (3)
∫ 1 x d x = 2 x + C (4)
∫ 1 x d x = ln | x | + C (5)
∫ 1 x 2 d x = − 1 x + C (6)
∫ x n d x = x n + 1 n + 1 + C ( n ≠ − 1 ) (7)
Интегралы от показательной функции и от гиперболических функций
Разумеется, формулу (8) (пожалуй, самую удобную для запоминания) можно рассматривать как частный случай формулы (9). Формулы (10) и (11) для интегралов от гиперболического синуса и гиперболического косинуса легко выводятся из формулы (8), но лучше просто запомнить эти соотношения.
∫ e x d x = e x + C (8)
∫ a x d x = a x ln a + C ( a > 0, a ≠ 1 ) (9)
∫ s h x d x = c h x + C (10)
∫ c h x d x = s h x + C (11)
Базовые интегралы от тригонометрических функций
Ошибка, которую часто делают студенты: путают знаки в формулах (12) и (13). Запомнив, что производная синуса равна косинусу, многие почему-то считают, что интеграл от функции sinx равен сosx. Это неверно! Интеграл от синуса равен "минус косинусу", а вот интеграл от cosx равен "просто синусу":
∫ sin x d x = − cos x + C (12)
∫ cos x d x = sin x + C (13)
∫ 1 cos 2 x d x = t g x + C (14)
∫ 1 sin 2 x d x = − c t g x + C (15)
Интегралы, сводящиеся к обратным тригонометрическим функциям
Формула (16), приводящая к арктангенсу, естественно, является частным случаем формулы (17) при a=1. Аналогично, (18) - частный случай (19).
∫ 1 1 + x 2 d x = a r c t g x + C = − a r c c t g x + C (16)
∫ 1 x 2 + a 2 = 1 a a r c t g x a + C ( a ≠ 0 ) (17)
∫ 1 1 − x 2 d x = arcsin x + C = − arccos x + C (18)
∫ 1 a 2 − x 2 d x = arcsin x a + C = − arccos x a + C ( a > 0 ) (19)
Более сложные интегралы
Данные формулы тоже желательно запомнить. Они также используются достаточно часто, а их вывод довольно утомителен.
∫ 1 x 2 + a 2 d x = ln | x + x 2 + a 2 | + C (20)
∫ 1 x 2 − a 2 d x = ln | x + x 2 − a 2 | + C (21)
∫ a 2 − x 2 d x = x 2 a 2 − x 2 + a 2 2 arcsin x a + C ( a > 0 ) (22)
∫ x 2 + a 2 d x = x 2 x 2 + a 2 + a 2 2 ln | x + x 2 + a 2 | + C ( a > 0 ) (23)
∫ x 2 − a 2 d x = x 2 x 2 − a 2 − a 2 2 ln | x + x 2 − a 2 | + C ( a > 0 ) (24)
Общие правила интегрирования
1) Интеграл от суммы двух функций равен сумме соответствующих интегралов: ∫ ( f ( x ) + g ( x ) ) d x = ∫ f ( x ) d x + ∫ g ( x ) d x (25)
2) Интеграл от разности двух функций равен разности соответствующих интегралов: ∫ ( f ( x ) − g ( x ) ) d x = ∫ f ( x ) d x − ∫ g ( x ) d x (26)
3) Константу можно выносить за знак интеграла: ∫ C f ( x ) d x = C ∫ f ( x ) d x (27)
Легко заметить, что свойство (26) - это просто комбинация свойств (25) и (27).
4) Интеграл от сложной функции, если внутренняя функция является линейной: ∫ f ( A x + B ) d x = 1 A F ( A x + B ) + C ( A ≠ 0 ) (28)
Здесь F(x) - первообразная для функции f(x). Обратите внимание: эта формула подходит только для случая, когда внутренняя функция имеет вид Ax + B.
Важно: не существует универсальной формулы для интеграла от произведения двух функций, а также для интеграла от дроби:
∫ f ( x ) g ( x ) d x = ? ∫ f ( x ) g ( x ) d x = ? (30)
Это не означает, конечно, что дробь или произведение нельзя проинтегрировать. Просто каждый раз, увидев интеграл типа (30), вам придется изобретать способ "борьбы" с ним. В каких-то случаях вам поможет интегрирование по частям, где-то придется сделать замену переменной, а иногда помощь могут оказать даже "школьные" формулы алгебры или тригонометрии.
Простой пример на вычисление неопределенного интеграла
Воспользуемся формулами (25) и (26) (интеграл от суммы или разности функций равен сумме или разности соответствующих интегралов. Получаем: ∫ 3 x 2 d x + ∫ 2 sin x d x − ∫ 7 e x d x + ∫ 12 d x
Вспомним, что константу можно выносить за знак интеграла (формула (27)). Выражение преобразуется к виду
3 ∫ x 2 d x + 2 ∫ sin x d x − 7 ∫ e x d x + 12 ∫ 1 d x
А теперь просто воспользуемся таблицей основных интегралов. Нам потребуется применить формулы (3), (12), (8) и (1). Проинтегрируем степенную функцию, синус, экспоненту и константу 1. Не забудем добавить в конце произвольную постоянную С:
3 x 3 3 − 2 cos x − 7 e x + 12 x + C
После элементарных преобразований получаем окончательный ответ:
x 3 − 2 cos x − 7 e x + 12 x + C
Проверьте себя дифференцированием: возьмите производную от полученной функции и убедитесь, что она равна исходному подинтегральному выражению.
Сводная таблица интегралов
| ∫ A d x = A x + C |
| ∫ x d x = x 2 2 + C |
| ∫ x 2 d x = x 3 3 + C |
| ∫ 1 x d x = 2 x + C |
| ∫ 1 x d x = ln | x | + C |
| ∫ 1 x 2 d x = − 1 x + C |
| ∫ x n d x = x n + 1 n + 1 + C ( n ≠ − 1 ) |
| ∫ e x d x = e x + C |
| ∫ a x d x = a x ln a + C ( a > 0, a ≠ 1 ) |
| ∫ s h x d x = c h x + C |
| ∫ c h x d x = s h x + C |
| ∫ sin x d x = − cos x + C |
| ∫ cos x d x = sin x + C |
| ∫ 1 cos 2 x d x = t g x + C |
| ∫ 1 sin 2 x d x = − c t g x + C |
| ∫ 1 1 + x 2 d x = a r c t g x + C = − a r c c t g x + C |
| ∫ 1 x 2 + a 2 = 1 a a r c t g x a + C ( a ≠ 0 ) |
| ∫ 1 1 − x 2 d x = arcsin x + C = − arccos x + C |
| ∫ 1 a 2 − x 2 d x = arcsin x a + C = − arccos x a + C ( a > 0 ) |
| ∫ 1 x 2 + a 2 d x = ln | x + x 2 + a 2 | + C |
| ∫ 1 x 2 − a 2 d x = ln | x + x 2 − a 2 | + C |
| ∫ a 2 − x 2 d x = x 2 a 2 − x 2 + a 2 2 arcsin x a + C ( a > 0 ) |
| ∫ x 2 + a 2 d x = x 2 x 2 + a 2 + a 2 2 ln | x + x 2 + a 2 | + C ( a > 0 ) |
| ∫ x 2 − a 2 d x = x 2 x 2 − a 2 − a 2 2 ln | x + x 2 − a 2 | + C ( a > 0 ) |
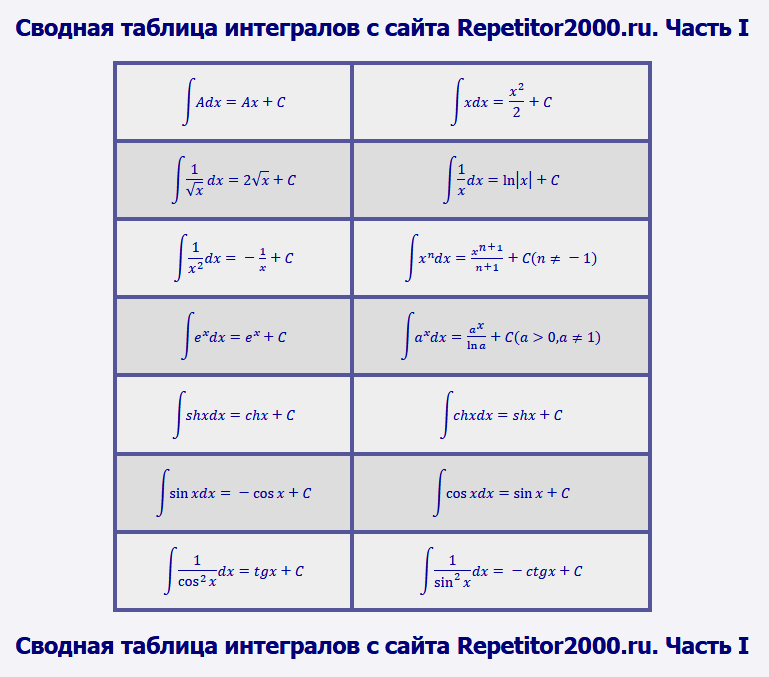
Скачайте таблицу интегралов (часть I) по этой ссылке

Скачайте таблицу интегралов (часть II) по этой ссылке
Если Вы учитесь в ВУЗе, если у Вас возникли сложности с высшей математикой (математический анализ, линейная алгебра, теория вероятностей, статистика), если Вам нужны услуги квалифицированного преподавателя, зайдите на страничку репетитора по высшей математике. Будем решать Ваши проблемы вместе!
Первообразная
Например, из справедливости равенства
вытекает, что функция F (x) = sin 2x является первообразной функции f (x) = 2 cos 2x .
Замечание . Функция F (x) = sin 2x не является единственной первообразной функции f (x) = 2 cos 2x , поскольку функция F (x) = sin 2x + 10 , или функция F (x) = sin 2x – 3 , или функции вида F (x) = sin 2x + c , где c – любое число, также являются первообразными функции f (x) = 2 cos 2x .
Справедлива следующая теорема, доказательство которой выходит за рамки школьного курса математики.
Теорема 1 . Если функция F (x) является первообразной функции f (x) на интервале (a, b) , то любая другая первообразная функции f (x) на интервале (a, b) имеет вид
где c – некоторое число.
Неопределенный интеграл
Определение 2 . Множество всех первообразных функции f (x) называют неопределенным интегралом от функции f (x) и обозначают
Если F (x) является первообразной f (x) , то в силу теоремы 1 смысл формулы (1) заключается в следующем:
Однако для упрощения формулу (2) принято записывать в виде
подразумевая, но не указывая специально, что c – любое число.
В формуле (3) функцию f (x) называют подынтегральной функцией, выражение f (x) dx нызывают подынтегральным выражением, а число c называют постоянной интегрирования.
Операцию вычисления (взятия) интеграла по известной подынтегральной функции называют интегрированием функции.
Правила интегрирования. Замена переменной в неопределенном интеграле
Вычисление интегралов (интегрирование) основано на применении следующих правил, которые непосредственно вытекают из правил вычисления производных.
Правило 1 (интеграл от произведения числа на функцию) . Справедливо равенство
где k – любое число.
Другими словами, интеграл от произведения числа на функцию равен произведению этого числа на интеграл от функции.
Правило 2 (интеграл от суммы функций) . Интеграл от суммы функций вычисляется по формуле
то есть интеграл от суммы функций равен сумме интегралов от этих функций.
Правило 3 (интеграл от разности функций) . Интеграл от разности функций вычисляется по формуле
то есть интеграл от разности функций равен разности интегралов от этих функций.
Правило 4 (интегрирование при помощи замены переменной) . Из справедливости формулы
Доказательство правила 4. Воспользовавшись формулой для производной сложной функции, вычислим производную от правой части формулы (4):
Мы получили подынтегральную функцию из левой части формулы (4), что и требовалось.
Замечание. Рассмотрим частный случай формулы (4), когда функция φ (x) является линейной функцией, то есть
и формула (4) принимает вид
Формула (5) часто используется при решении задач.
Таблица интегралов
где n – любое число, не равное – 1
где a – любое положительное число, не равное 1
где a – любое положительное число, не равное 1
где n – любое число, не равное – 1 .
где a – любое положительное число, не равное 1 .
где a – любое положительное число, не равное 1
Примеры решения задач
| F (x) = 4 cos x + c, | (6) |
Подставляя в формулу (6) значение x = 0 , находим значение постоянной интегрирования c :
для функции φ (x) = cos x , получаем
Подставляя в формулу (7) значение x = 2π , находим значение постоянной интегрирования c :
для функции φ (x) = e x , получаем
| Производная | Функция | Первообразная | |
|---|---|---|---|
| f '(x) | f(x) | F(x) | |
| 1. | 0 | C | Cx |
| 2. | 1 | x | x 2 _ 2 |
| 3. | n x n−1 | x n | x n+1 ____ n+1 , n ≠ −1 |
| 4. | 1 ___ 2 √x _ | √x __ | * |
| 5. | − 1 __ x 2 | 1 _ x | ln x |
| 6. | e x | e x | e x |
| 7. | a x ln a | a x | a x __ ln a |
| 8. | 1 _ x | ln x | * |
| 9. | 1 ____ x ln a | logax | * |
| 10. | cos x | sin x | − cos x |
| 11. | − sin x | cos x | sin x |
| 12. | 1 _____ cos 2 x | tg x | * |
| 13. | * | 1 _____ cos 2 x | tg x |
| 14. | − 1 _____ sin 2 x | ctg x | * |
| 15. | * | 1 _____ sin 2 x | − ctg x |
| 16. | 1 _____ √1−x 2 ____ | arcsin x | * |
| 17. | * | 1 _____ √1−x 2 ____ | arcsin x |
| 18. | − 1 _____ √1−x 2 ____ | arccos x | * |
| 19. | 1 _____ 1 + x 2 | arctg x | * |
| 20. | * | 1 _____ 1 + x 2 | arctg x |
| 21. | − 1 _____ 1 + x 2 | arcctg x | * |

Полагаю, что посетитель этой страницы уже не единожды обращался и, скорее всего, пытался выучить наизусть таблицы производных и первообразных основных элементарных функций. Вместо таблицы первообразных Вы могли учить простейшие табличные интегралы, что, фактически, одно и то же. На мой взгляд, для вычисления неопределенных интегралов эффективнее пользоваться совмещенной таблицей, заодно это позволит быстрее её запомнить.
В таблице нет столбика для табличных интегралов по понятным причинам: неопределенный интеграл - совокупность первообразных, отличающихся друг от друга на постоянную величину. Этот столбик отличался бы от предыдущего только добавлением к первообразной одного слагаемого - произвольной постоянной "+ С". При этом функцию следовало бы поместить под знак интеграла. Всё это несущественно для запоминания формул.
Звёздочки в некоторых ячейках таблицы не означают, что у этой функции нет производной или первообразной. (Хотя такое случается, но не с приведенными элементарными функциями.) Здесь звёздочки заменяют производные и первообразные, которые выражаются композицией функций, а потому не подлежат запоминанию. Напротив, на экзамене вас могут попросить вычислить их, пользуясь, соответственно, правилами дифференцирования или методами интегрирования функций. Примеры вычисления некоторых из них представлены ниже таблицы. Остальные используются для упражнений в разделе о вычислении интегралов.

Если потребуется распечатать таблицу для использования, то лучше скачать её в формате рисунка. Тогда Вы сможете разместить его на листе формата А4 желаемым способом.
а) По правилу дифференцирования дроби
б) С использованием свойств степеней
Как показывает практика, большинство студентов предпочитает первый способ, но при этом чаще ошибается в вычислениях. Я рекомендую освоить второй подход, однако производная это тема другой статьи.
При вычислении использовались непосредственное интегрирование, свойства степенной функции и формулы для её первообразной (строка 3 таблицы). 
Итак, одной из первообразных квадратного корня является функция 2x √x _ ____ 3 , её можно поместить в таблицу вместо звёздочки в этой строке.
Вообще говоря, все пять верхних строк таблицы относятся к степенным функциям, поэтому их можно было бы заменить одним правилом:
- при дифференцировании степенной функции показатель степени сначала выносится коэффициентом перед ней, затем уменьшается на единицу;
- при интегрировании степенной функции показатель степени сначала увеличивается на единицу, затем сносится в знаменатель дроби.
Последнее верно для любых целых, дробных и отрицательных степеней, кроме n = −1, иначе в знаменатель пришлось бы помещать 0.
Если производная функции arccosx это функция 
, то по определению первообразная функции 
это функция arccosx , которая по праву может занять своё место в таблице.
Но с таким же успехом мы можем считать, что 
это производная функции arcsinx , умноженная на −1, и тогда её первообразной следует считать функцию −arcsinx ?
Действительно, так как arcсosx и −arcsinx отличаются только на константу, то они относятся к одному и тому же неопределенному интегралу, а значит как первообразные взаимозаменяемы. Не имеет смысла учить две формулы, когда достаточно запомнить одну, если вы понимаете смысл происходящего.
arcsinx + arcсosx = π _ 2 ,
так как по сути это два острых угла одного и того же прямоугольного треугольника.
То же самое относится к функции arcctgx.

Читайте также:


