Все о векторах шпора

Открываемый курс уроков по геометрии не претендует на теоретическую полноту, он ориентирован на решение практических задач. Я включу в свои лекции только то, что с моей точки зрения, является важным в практическом плане. Если вам необходима более полная справка по какому-либо подразделу, рекомендую следующую вполне доступную литературу:

1) Вещь, с которой, без шуток, знакомо несколько поколений: Школьный учебник по геометрии, авторы – Л.С. Атанасян и Компания. Сия вешалка школьной раздевалки уже выдержала 20 (!) переизданий, что, конечно, не является пределом.

2) Геометрия в 2 томах. Авторы Л.С. Атанасян, Базылев В.Т. Это литература для высшей школы, вам потребуется первый том. Из моего поля зрения могут выпадать редко встречающиеся задачи, и учебное пособие окажет неоценимую помощь.

Из инструментальных средств предлагаю собственную разработку – программный комплекс по аналитической геометрии, который значительно упростит жизнь и сэкономит массу времени.

Предполагается, что читатель знаком с базовыми геометрическими понятиями и фигурами: точка, прямая, плоскость, треугольник, параллелограмм, параллелепипед, куб и т.д. Желательно помнить некоторые теоремы, хотя бы теорему Пифагора, привет второгодникам)

А сейчас мы последовательно рассмотрим: понятие вектора, действия с векторами, координаты вектора. Далее рекомендую прочитать важнейшую статью Скалярное произведение векторов, а также Линейная (не) зависимость векторов. Базис векторов и Векторное и смешанное произведение векторов. Не лишней будет и локальная задача – Деление отрезка в данном отношении. На основе вышеуказанной информации можно освоить уравнение прямой на плоскости с простейшими примерами решений, что позволит научиться решать задачи по геометрии. Также полезны следующие статьи: Уравнение плоскости в пространстве, Уравнения прямой в пространстве, Основные задачи на прямую и плоскость, другие разделы аналитической геометрии. Естественно, попутно будут рассматриваться типовые задания.

Более того, по материалам сайта создана книга!

. да, это свершилось! – освойте азы теории и научитесь решать в кратчайшие сроки! Спасибо за поддержку проекта.

Понятие вектора. Свободный вектор

. Примечание: Здесь и далее можете считать, что векторы лежат в одной плоскости или можете считать, что они расположены в пространстве – суть излагаемого материала справедлива и для плоскости и для пространства.

То была стилистика, а сейчас о способах записи векторов:

Как находить длину вектора мы узнаем (или повторим, для кого как) чуть позже.

То были элементарные сведения о векторе, знакомые всем школьникам. В аналитической же геометрии рассматривается так называемый свободный вектор.

Если совсем просто – вектор можно отложить от любой точки: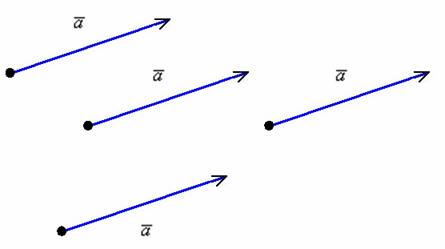

Следует отметить, что с точки зрения физики понятие свободного вектора в общем случае некорректно, и точка приложения имеет значение. Действительно, прямой удар одинаковой силы по носу или по лбу хватит развивать мой дурацкий пример влёчет разные последствия. Впрочем, несвободные векторы встречаются и в курсе вышмата (не ходите туда :)).

Далее, если не оговаривается иное, речь пойдёт только о свободных векторах.

Действия с векторами. Коллинеарность векторов

В школьном курсе геометрии рассматривается ряд действий и правил с векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др. Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.

Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.

Правило умножения вектора на число легче понять с помощью рисунка: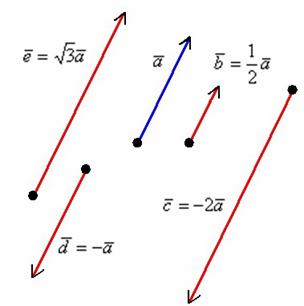

Разбираемся более детально:

С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.

Координаты вектора на плоскости и в пространстве

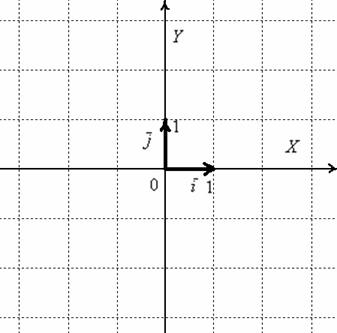
Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости. Что такое базис, думаю, интуитивно многим понятно, более подробную информацию можно найти в статье Линейная (не) зависимость векторов. Базис векторов. Простыми словами, базис и начало координат задают всю систему – это своеобразный фундамент, на котором кипит полная и насыщенная геометрическая жизнь.

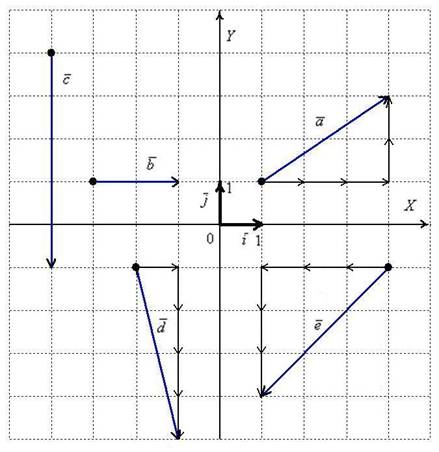
! ВСЕМ настоятельно рекомендую прочитать ВСЁ!

То есть, в круглых скобках указываются координаты вектора. В практических задачах используются все три варианта записи.

С координатами на плоскости разобрались. Теперь рассмотрим векторы в трехмерном пространстве, здесь практически всё так же! Только добавится ещё одна координата. Трехмерные чертежи выполнять тяжко, поэтому ограничусь одним вектором, который для простоты отложу от начала координат: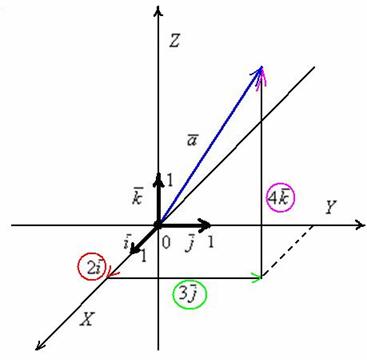

Вот, пожалуй, и все минимальные теоретические знания, необходимые для решения задач аналитической геометрии. Возможно многовато терминов и определений, поэтому чайникам рекомендую перечитать и осмыслить данную информацию ещё раз. Да и любому читателю будет полезно время от времени обращаться к базовому уроку для лучшего усвоения материала. Коллинеарность, ортогональность, ортонормированный базис, разложение вектора – эти и другие понятия будут часто использоваться в дальнейшем. Отмечу, что материалов сайта недостаточно для сдачи теоретического зачета, коллоквиума по геометрии, так как все теоремы (к тому же без доказательств) я аккуратно шифрую – в ущерб научному стилю изложения, но плюсом к вашему пониманию предмета. Для получения обстоятельной теоретической справки прошу следовать на поклон к профессору Атанасяну.

А мы переходим к практической части:

Простейшие задачи аналитической геометрии.
Действия с векторами в координатах

Задания, которые будут рассмотрены, крайне желательно научиться решать на полном автомате, а формулы запомнить наизусть, даже специально не запоминать, сами запомнятся =) Это весьма важно, поскольку на простейших элементарных примерах базируются другие задачи аналитической геометрии, и будет досадно тратить дополнительное время на поедание пешек. Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.

Изложение материала пойдет параллельным курсом – и для плоскости, и для пространства. По той причине, что все формулы… сами увидите.

То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора.

Лично я привык к первой версии записи.

По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения некоторых моментов чайникам, не поленюсь: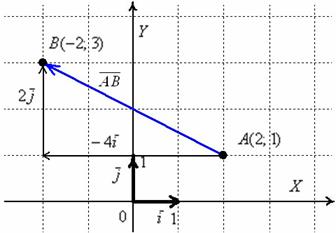

Обязательно нужно понимать различие между координатами точек и координатами векторов:

Координаты точек – это обычные координаты в прямоугольной системе координат. Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.

Дамы и господа, набиваем руку:

Пожалуй, достаточно. Это примеры для самостоятельного решения, постарайтесь ими не пренебрегать, окупится ;-). Чертежи делать не нужно. Решения и ответы в конце урока.

Длина, как уже отмечалось, обозначается знаком модуля.

Для наглядности выполню чертёж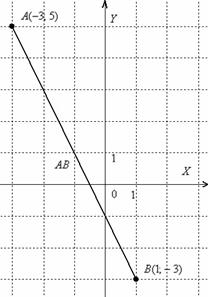

Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:

Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:

Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.

В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.

Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.

Задание для самостоятельного решения с отрезком в пространстве:

Решение и ответ в конце урока.

Данные формулы (как и формулы длины отрезка) легко выводятся с помощью небезызвестной теоремы Пифагора.

Я взял те же точки, что и в Примере 3.

Выполним чертеж к задаче: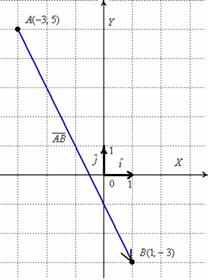

Этот способ широко практикуется в ходе решений задач аналитической геометрии.

Вышесказанное справедливо и для пространственного случая

Решения и ответы в конце урока.

В первой части урока мы рассматривали правила сложения векторов и умножения вектора на число. Но рассматривали их с принципиально-графической точки зрения. Посмотрим, как данные правила работают аналитически – когда заданы координаты векторов:

Приведённые факты строго доказываются в курсе аналитической геометрии.

Для векторов в пространстве можно провести аналогичные выкладки. Но там чертежи строить значительно сложнее, поэтому ограничусь аналитическим решением (на практике, собственно, бОльшего и не надо):

И в заключение занятный пример с векторами на плоскости:

Это задача для самостоятельного решения.

Какой вывод? Многие задачи аналитической геометрии прозрачны и просты, главное, не допустить вычислительных ошибок. Следующие рекомендуемые к изучению уроки:

Это, так скажем, вектор-минимум студента =)

Любите векторы, и векторы полюбят вас!

Решения и ответы:

(Переход на главную страницу)

Величины, которые полностью определяются заданием направления численного значения называются векторами. (Скаляры - числа).

С этого момента вектор будет обозначаться ( AB` ).

AB`, a` - векторы. (рисунок – вектор, начало, конец). Длинна вектора называется модулем вектора. AB = |AB`| = |a`|. Вектор, у которого совпадает начало и конец, называется нулевым вектором. 0`, | 0`| = 0;

Вектор, модуль которого равен 1, называется единичным вектором |e`|= 1.

2 вектора, лежащие на одной прямой или на параллельной прямой называются колинеарными. 2 вектора называются равными, если они:

1) колинеарны, 2) они имеют одно направление, 3) |a`|=|b`|;

a`=λb` (рисунки и примеры)

Алгебраические операции с векторами.

1
) Сложение векторов. c` = a` + b` (рисунок – сложение по правилу параллепипеда).

2) Суммой a` и b` называется 3ий вектор c`, соединяющий начало одного и конец другого вектора. (рисунок - сложение по правилу треугольника, 2 вектора выходят из одной точки).

3) Разность 2х векторов. Разностью 2х векторов a` и b` называется 3ий вектор c`, который в сумме с вычитаемым b` дает a`.

c`=a` +b`; d`= a`-b` (рисунок – вычитание и сложение).

Чтобы |a` + b`| = |a` - b`| необходимо: a ┴ b.

Умножение вектора на число. Дано: a`, λ; b` = λ a`; λ (a` + b`) = λa` ± λb`;

a`(λ1 + λ2) = λ1 a` + λ2 a`; Угол между векторами. Это наименьший угол, на который нужно повернуть один из векторов против часовой стрелки до их полного совпадения.

Проекция вектора на ось. Составляющие вектора на оси.

П
усть дана произвольная ось l . Состовляющие AB` на оси l. Составляющие векторы: A’B’` = x2 – x1; A’B’ = проекция l AB` - проекция AB на ось l.

φ=π/2; x2 > x1; x2 – x1 > 0; π/2 0;

λ1<>0; μ1=λ2/λ1; μ2=λ3/λ2… ; a1`= μ1 a2`+μ2 a3` +…+μ<sub>(n - 1)</sub> an`;

Вектор a1` представлен линейной комбинацией векторов.

Д
окажем следующую ТЕОРЕМУ: Всякие 3 вектора на плоскости линейно зависимые. Дано: a`, b`, c`, причем 2 из них колинеарны. Док-ть: a`=λ1 b`+λ2 c`-?; Док-во: 1) пусть a` и b` колинеарны: a`=λ1 b` + 0 c`; λ1<>0; λ2=0; c`=λ1 a`+λ2 b`=|b`=αa`|=λ1 a`+λ2 α a` = β a` + 0 b`; 2) Дано: a`, b`, c`; c`=λ1 a`+λ2 b`; Док-во: c`=OM`; OM` = OM1`+OM2`; OM1`=λ1 a`; OM2`=λ2 b`; c`=λ1 a` + λ2 b`

Следствие: 1. Максимальное число линейно-независимых векторов на плоскости равно двум. 2. Для того, чтобы 2

вектора на плоскости были линейно-независимы , чтобы они были неколлинеарными.

Линейная зависимость векторов в трехмерном пространстве. Вектора, лежащие в одной плоскости или параллельных плоскостях называются компланарными. ТЕОРЕМА: любые 4 вектора в 3х-мерном пространстве являются линейно-зависимыми. Дано: a`, b`, c`, d`; из них 3 компланарны; a` = λ1 b` +λ2 c` +0` d` (см. рисунок).

O
M`= a`; a` ^ b`; d` ^ b`; b` ^ c`; ON – проекция

ON`= OM2+ON3; NM`=OM1`;

OM1`=λ1 d`; OM2`=λ2 b`; OM3 = λ3 c`;

Это означает, что векторы линейно-зависимые.

1. Максимальное число линейно-независимых

векторов в трехмерном пространстве равно 3м.

2. Для того, чтобы 3 вектора в трехмерном пространстве были линейно-независимые , чтобы они были не компланарны.

Базис в пространстве. Любые 2 линейно-независимых вектора на плоскости образуют базис. Любой тертий вектор можно выразить через базис: b`, c`; a`=λ1 b`+λ2 c`; λ1, λ2 – афинные координаты вектора a` в базисе b` и c`. ТЕОРЕМА: Разложение по базису является единственным. Дано: базис b`, c`. Допустим, что разложение вектора по базису возможно в двух вариантах: a`=λ1 b`+λ2 c` <λ1, λ2>; a`=β1 b`+β2 c` <β1, β2>; 0`= (λ1 – β1) b`+ (λ2 – β2) c`; x1 – β1 = 0; x2 – β2 = 0; x1 = β1; λ2 = β2.

ТЕОРЕМА: Любые 3 линейно-независимые вектора образуют базис и разложение по базису в трехмерном пространстве является единственным.

n-мерное пространство. Размерность пространства. Любые n линейно-независимых векторов в n-мерном пространстве образуют базис. Размерность пространства определяется числом линейно-независимых векторов в пространстве. 2  R2; 3 R3; nRn; a` (λ1..λn).

В статье узнаете что такое вектор, векторные компоненты, единичный вектор, как складывать вектора, умножать вектора на скаляр, скалярное, векторное и смешанное произведение двух векторов.

Сохранение физической величины с вектором обычно означает совершенно иную ситуацию, чем просто сохранение ее скалярной длины. Постоянное значение импульса p (скаляр) может означать совершенно иную ситуацию, чем постоянный вектор p.

Вектор должен иметь три необходимые характеристики: значение (длина), направление, начало и конец.

Любое изменение любого из этих признаков — длины, направления или начало с концом — означает, что создан другой вектор. Два вектора равны тогда и только тогда, когда они имеют равную длину, направление и начало с концом.

Векторные компоненты

Компонентами вектора являются его проекции на оси системы координат.

Также в трехмерном пространстве векторы A называются векторами, которые являются проекциями этого вектора A на оси системы координат.

Имея вектор A, мы погружаем его в систему координат x, y, z. Векторы, являющиеся проекциями вектора A на оси системы, называются векторными компонентами вектора A. Вектор A является векторной суммой составляющих векторов A_x, A_y и A_z .

Единичный вектор

Единичный вектор, имеющий то же направление, что и вектор, на который он ссылается, важен, но его длина всегда равна 1.

Единичные векторы осей координат. Мы также присваиваем единичные векторы оси системы отсчета. а) относится к правовращающей системе и б) к левосторонней системе.

Сложение векторов

Сумма вектора обычно не совпадает с суммой скалярных величин:

Добавление двух или более векторов друг к другу сводится к добавлению их компонентов, то есть проекций на опорные оси. Результирующий вектор называется случайным вектором. Для двух векторов результирующий вектор является диагональю параллелограмма, построенного на этих векторах. Метод параллелограмма.

В случае большего числа векторов результирующий вектор получается путем рисования одного из этих векторов, затем в конце первого вектора мы начинаем второй, в конце второго мы даем начало третьего и так далее. Полученный вектор является вектором, начало которого находится в начале первого из добавленных векторов. и его конец в конце последнего. При изменении порядка сложения результирующий вектор (красный) не меняет длину, направление:

Это правило добавления векторов также действует в трехмерном пространстве:

Умножение вектора на скаляр

Самым простым умножением, выполняемым на векторах, является умножение вектора на скаляр (число). Такое умножение не меняет направление вектора, но, как правило, меняет его длину и может изменить его конец (когда скаляр является отрицательным числом). Когда вектор A умножается на α-скаляр, мы получаем новый вектор B:

Скалярное произведение и векторное произведение двух векторов являются очень важными направления в физике и геометрии. Существует также смешанное произведение трех векторов.

Скалярное произведение двух векторов

Формально скалярное произведение векторов представляет собой точку, и ее значение определяется зависимостью

Скалярное произведение описывает способ, которым оба вектора видят друг друга, то есть как долго тень (проекция) отбрасывает каждый из векторов в своего партнера, когда угол между ними равен φ

B cos φ — длина тени, которую вектор B выбрасывает в вектор A. Аналогично, A cos φ — длина тени, которую вектор A выбрасывает в вектор B.

Когда длина проекции (тени) одного из векторов равна нулю, тогда длина проекции второго вектора равна нулю, то есть A • B = 0. Это означает, что эти векторы не работают в одном и том же направлении вообще. Работа, которую мы выполняем при движении автомобиля, зависит не только от приложенной силы F, но и от угла, который создает направление силы и направление пути.

Так как единичные векторы оси системы отсчета х, у и z, которые обозначают векторы е_х, е_Y и е_z, перпендикулярны друг к другу, то в виду того, что А • В = АВcosφ и что cos 0 = 1 и cos 90 o = 0, мы получаем произведение значений этих единичных векторов:

Выполнение аналогичного умножения на векторы A и B

мы получили новое выражение для скалярного произведения двух векторов A и B

Значение скалярного произведения двух векторов A и B можно записать в виде двух эквивалентных выражений:

Сравнивая оба выражения, мы находим выражение для угла между векторами A и B:

Векторное произведение двух векторов

Многие важные величины в науке и технике определяются вектором, который является произведением двух других векторов. В таких случаях произведение этих векторов, называемое векторным произведением , приводит к третьему вектору.

В этом случае задача состоит в том, чтобы определить все три особенности вектора C, являющегося произведением векторного произведения векторов A и B:

• длина
• направление
• начало и конец

Произведение векторов A и B , приводящее к третьему вектору C, отмечено диагональным крестом

Направление

Вектор С такой, что вектор перпендикулярен к плоскости, образованной векторами A и B, которая перпендикулярна как к вектору A и B.

Длина

вектор С равен значению параллелограмма, построенного на векторах А и В. Числовой C = ABsin φ.

Начало и конец

Вектор С определяет правое направление движения шнека во время нанесения первого вектора, а именно А или B.

Изменение порядка применения векторов означает изменение знака векторного произведения.

Таким образом, действительное свойство векторного произведения выглядит следующим образом A*B= -B*A

В отличие от скалярного произведения, векторное произведение некоммутативно.

Мы встретимся с векторным произведением на протяжении всего курса физики. Это также часто встречается в механике, а также в науке об электричестве и магнетизме.

В повседневной жизни векторное произведение находится в виде момента силы во вращательном движении. Мы воздействуем на вращательное движение тем эффективнее, чем больше применяем момент силы.

При откручивании гайки гаечным ключом речь идет не только о силе F, но и о способе ее применения (длина рычага R и угол, который создает рычаг с направлением силы).

Все эти зависимости элегантно включены в одно выражение в виде векторного произведения:

Хотя составляющие вектора C, который является произведением векторного произведения векторов A и B, уже включены в его длину и направление, но имея данные составляющих векторов A и B, мы можем использовать их для определения компонентов вектора C в форме матрицы:

Удобнее всего рассчитать этот определитель, расширив относительно первой строки.

Смешанное произведение трех векторов

Смешанное произведение трех векторов является скалярным значением, равным значению детерминанта

Геометрическая интерпретация: смешанное произведение численно равно объему V параллелепипеда, растянутому по векторам A, B и C:

Циклическая корректировка векторов в смешанном произведении не меняет значение этого произведения, то есть:

Шпаргалки по математике, алгебре и геометрии Шпаргалки по физике / Шпаргалки по химии

Шпаргалки по математике, алгебре и геометрии

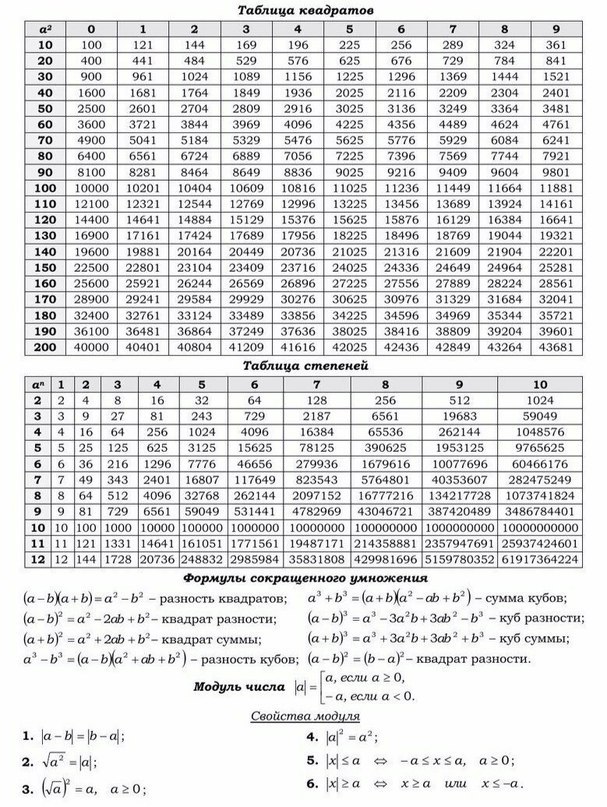
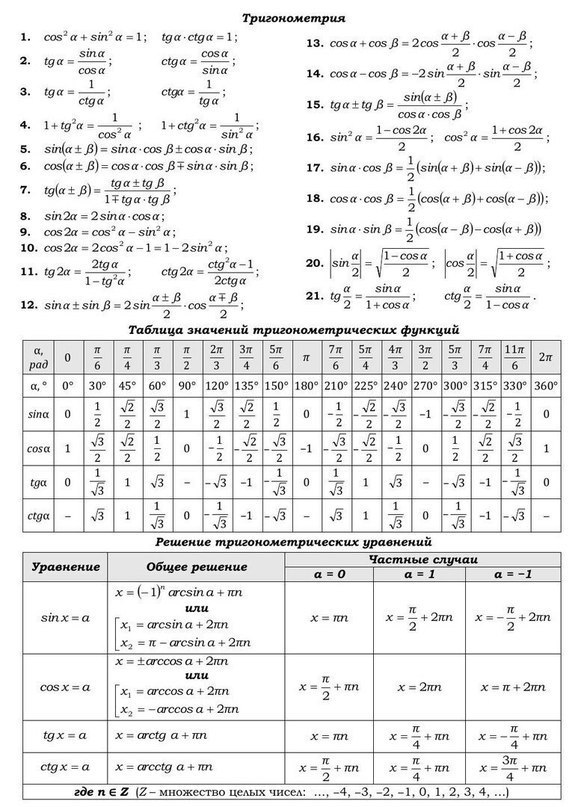
Таблица квадратов. Таблица степеней. Формулы сокращенного умножения. Модуль числа. Свойства модуля:	Уравнения и неравенства с модулем. Последовательности и прогрессии. Метод кординат на плоскости. Скалярное произведение векторов. Расстояние между точками.	Тригонометрия - основные формулы. Таблица значений тригонометрических функций. Решение тригонометрических уравнений:	Четность и нечетность тригонометрических функций. Обратные тригонометрические функции. Формулы приведения. Знаки тригонометрических функций. Показательные уравнения и неравенства.
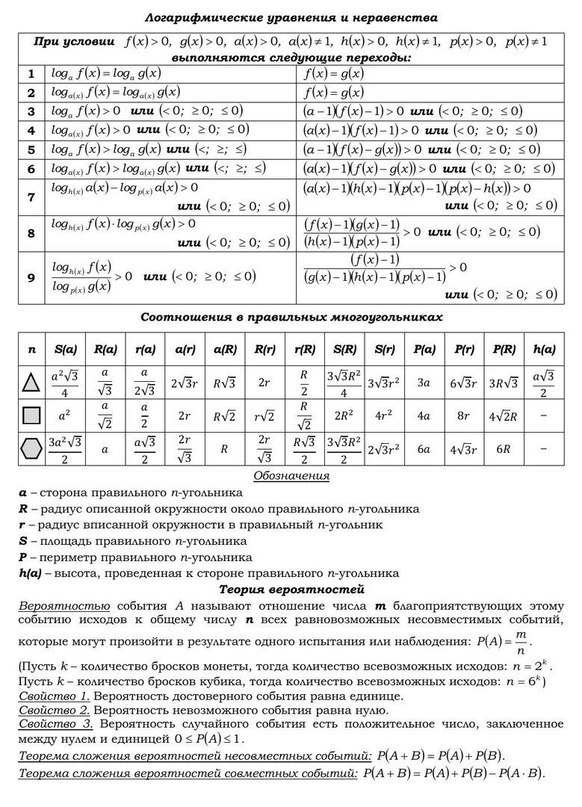
Корень n-ой степени. Степени. Иррациональные уравнения и неравенства. Логарифм, свойства логарифмов	Логарифмические уравнения и неравенства. Соотношения в правильных многоугольниках. Теория вероятностей. Теоремы сложения вероятностей.	Логарифмические уравнения и неравенства.	Производная. Правила дифференцирования. Производная сложной функции. Уравнение касательной к графику функции в точке.
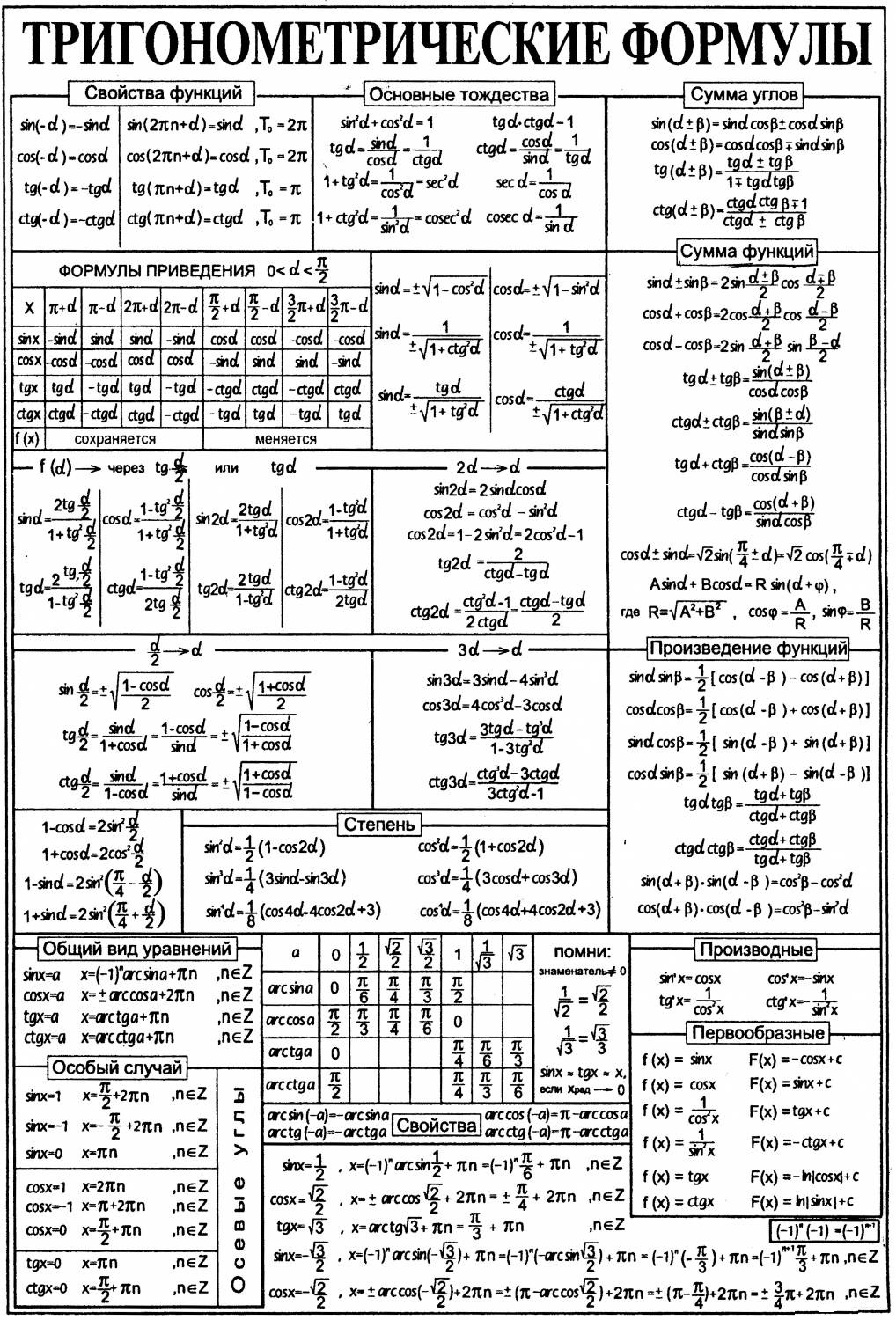
Тригонометрические формулы. Свойства функций, основные тождества, сумма углов. Сумма функций, формулы приведения, особые случаи, степени, половинные, двойные и тройные углы. Обратные функции.

Набор 2 - Алгебра. Линейная алгебра.
Свойства степеней. Формулы сокращенного умножения. Свойства арифметических корней. Модуль. Начала математического анализа: прогрессии арифметическая и геометрическая. Производная. Первообразная и интеграл. Среднее арифметическое и среднее геометрическое.	Тригонометрия. Основные формулы. Арксинус, арккосинус, арктангенс, арккотангенс. Четность функций. Значения тригонометрических функций некоторых углов.	Графики некоторых элементарных функций. Логарифмы. Решение квадратных, иррациональных, показательных, тригонометрических уравнений, уравнений с модулем	Квадратные неравенства. Неравенства с модулем. Логарифмические неравенства. Неравенства с модулем. Иррациональные неравенства. Показательные неравенства. Комбинаторика и бином Ньютона.
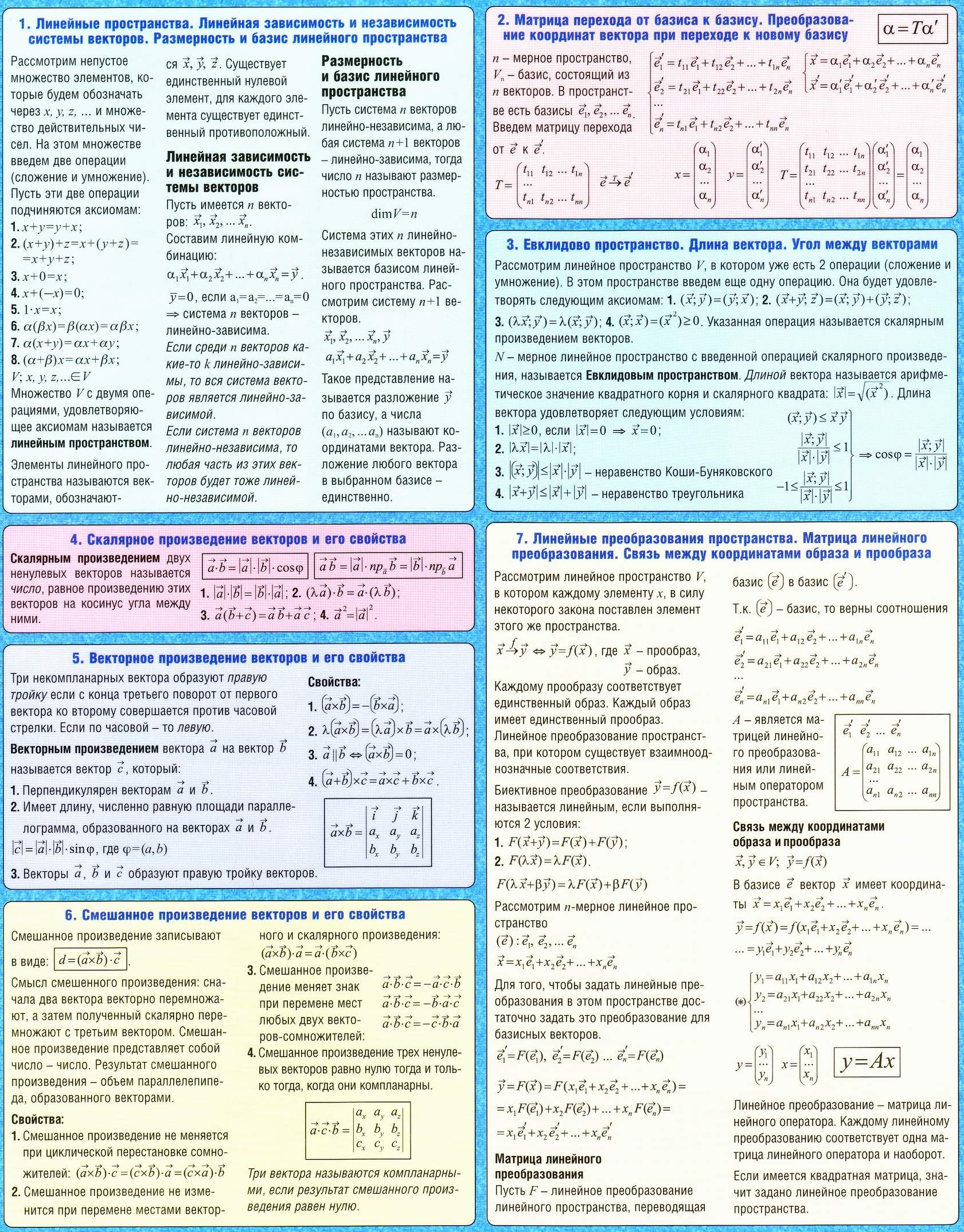
Определение комплексного числа. Геометрическая интерпретация комплексного числа. Тригонометрическая форма комплексного числа. Показательная форма комплексного числа. Действия с комплексными числами. Последовательности, пределы последовательности. Теоремы о пределах числовых последовательностей.	Определение предела числовой функции. Односторонние пределы. Свойства пределов. Непрерывные функции и их свойства. Точки разрыва и их классификации. Замечательные пределы. Важные пределы. Теоремы о среднем. Правило Лопиталя.	Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства. Скалярное и векторное произведение векторов. Смешанное произведение векторов. Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису. Евклидово пространство. Длина вектора. Угол между векторами. Линейные преобразования пространства. Матрица линейного преобразования. Связь между координатами образа и прообраза.	Связь между координатами одного и того же линейного оператора в разных базисах. Угол между прямой и плоскостью. Расстояние от точки до плоскости. Характеристические уравнения линейного оператора. Собственные векторы линейного оператора и их свтойства. Поверхности второго порядка. Плоскость в пространстве. Виды углов в пространстве. Уравнения плоскости.
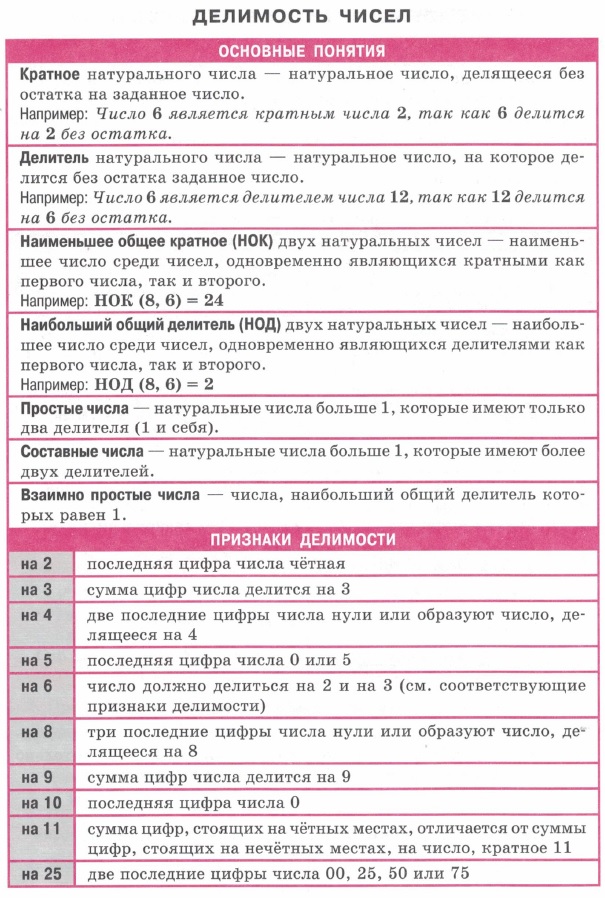
Делимость чисел. Кратное. Делитель. НОК. НОД Простые и составные числа. Взаимно простые числа.	Числовые последовательности, члены, способы задания. Арифметическая и геометрическая прогрессии. Формулы. Характеристические свойства	Числа. Множества натуральных, целых, рациональных, действительных, иррациональных чисел. Арифметические действия с дробями. Модуль - свойства.	Решение квадратных уравнений. Формулы дискриминанта. Решение неполных квадратных уравнений. Теорема Виета. Алгоритм решения квадратного неравенства.
Основные свойства функций. Понятие функции. Четность и нечетность. Периодичность. Нули функции. Промежутки знакопостоянства. Монотонность (возрастание, убывание). Асимптоты. Алгоритм описания фукнкции.		Преобразование графиков функций у= f(x) в y=-f(x); y=f(-x); y=-f(-x); y=f(x-a); y=f(x)+b; y=f(ax); y=kf(x); y=|f(x)|; y=f(|x|). Построение графика обратной функции Степенные функции y=xn и y=x1/n, n∈Z. Свойства, графики. Квадратичная функция. Свойства степеней. Свойства арифметических корней. Формулы сокращенного умножения. Примеры значения степенных функций. Неравенства, понятия, строгие, нестрогие, решение. Свойства неравенств. Решение линейных неравенств. Решение квадратных неравенств. Метод интервалов при решении неравенств. Решение показательных неравенств. Решение логарифмическмх неравенств. Решение иррациональных неравенств. Решение неравенств с модулем. Часто применяемые неравенства Интегрирование функций. Понятие и основное свойство первообразной. Неопределенный интеграл. Правила интегрирования. Определенный интеграл. Формула Ньютона-Лейбница. Свойства и геометрический смысл определенного интеграла. Физический смысл определенного интеграла Уравнения прямой на плоскости. Общее уравнение прямой. Уравнение прямой "в отрезках". Уравнение прямой с угловым коэффициентом. Уравнение пучка прямых, проходящих через точку. Уравнение прямой, проходящей через 2 точки. Нормальное уранение прямой. Консультации и техническая поддержка сайта: Zavarka Team Читайте также: Может ли на узи оценить кости Ходьба при реактивном артрите Массаж для голосовых связок Договора коммерческого найма жилого помещения шпора Какие паразиты вызывают ревматоидный артрит Пожалуйста, не занимайтесь самолечением! При симпотмах заболевания - обратитесь к врачу.