Теоремы по геометрии 7 класс с доказательством шпоры

Геометрия 7 класс

1) Смежными углами называют два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой;

2) Вертикальными угламиназываются углы если стороны одного угла являются продолжениями другого.

3) Перпендикулярными прямыминазываются две пересекающиеся прямые, если они образуют четыре прямых угла.

4) Периметром треугольниканазывается сумма длин всех сторон.

5) Первый признак треугольника:Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

6) Перпендикуляр к прямой: Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой и при том только один.

7) Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

8) Биссектрисой треугольника называетсяотрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

9) Высотой треугольника называетсяперпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

10) Замечательное свойство треугольника:В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения так же пересекаются в одной точке.

11) Равнобедренным треугольником называется треугольник, если две его стороны равны.

12) Равные стороны равнобедренного треугольниканазываются боковыми сторонами, а третья сторона – основанием.

13) Равносторонним треугольником называется треугольник, все стороны которого равны.

14) 1 свойство равнобедренного треугольника: в равнобедренном треугольнике углы при основании равны.

15) 2 свойство равнобедренного треугольника: в равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

16) Следствие 1:Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.

17) Следствие 2: Медианаравнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой.

18) Второй признак равенства треугольника:Если сторона, и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

19) Третий признак равенства треугольников: Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

20) Параллельными прямыми называютсядве прямые, лежащие на плоскости, если они не пересекаются.

21) Признаки параллельности двух прямых: 1)Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. 2)Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. 3)Если при пересечении двух прямых секущей сумма односторонних углов равна 180 градусов, то прямые параллельны.

22) Аксиомами называются исходные положения в геометрии.

23) Аксиомы: 1)Через любые две точки проходит прямая, и при том только одна. 2)На любом луче от его начала можно отложить отрезок, равный данному, и при том только один. 3)От любого луча, в заданную сторону можно отложить угол, равный данному, не развёрнутому углу, и при том только один.

24) Аксиомы параллельных прямых:Через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.

25) Следствие 1:Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

26) Следствие 2: Если две прямые параллельны третьей прямой, то они параллельны.

27) Теорема об углах, образованных двумя параллельными прямыми и секущей:

Теорема 1:Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Следствие 1:Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.

Теорема 2: Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Теорема 3: Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусов.

28) Теорема о сумме углов треугольников:Сумма углов треугольников равна 180 градусов.

29) Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

30) В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой, или прямой.

31) Треугольник называется остроугольным,если все три угла острые.

32) Треугольник называется тупоугольным,если один из углов тупой.

33) Треугольник называется прямоугольным,если один из углов прямой.

34) Гипотенуза -это сторона прямоугольного треугольника, лежащая против прямого угла.

35) Катет – это другая сторона прямоугольного треугольника.

36) Теорема о соотношении между сторонами и углами треугольника: 1) В треугольнике против большей стороны лежит больший угол; 2) Против большего угла лежит большая сторона.

Следствие 1: В прямоугольном треугольнике гипотенуза больше катета.

Следствие 2: Если два угла треугольника равны, то треугольник равнобедренный.

Каждая сторона треугольника меньше суммы двух других сторон

Следствие:Для любых трёх точек А, В, С не лежащих на одной прямой справедливо неравенство: АВ

Математику уж затем учить надо, что она ум в порядок приводит

Теорема 1: Две прямые, перпендикулярные к третьей, не пересекаются.


Доказательство от противного. Есть две прямые АА1 и ВВ1 перпендикулярны к прямой PQ одновременно. Предположим, что, продолжая прямые, можно достичь некоторой точки M, в которой они пересекаются. Перегнем плоскость вдоль прямой PQ. В этом случае углы при данных прямых накладываются друг на друга, а наложенные лучи совпадают. При этом точка М, получит проекцию некоторой точки M1 (при пересечения АА1 и ВВ1 в нижней полуплоскости) . Это будет означать, что две прямые АА1 и ВВ1 пересекаются в двух точках М и М1. Но через любые две точки на плоскости можно провести только одну прямую! Таким образом, предположение о том, что данные прямые пересекаются неверно. Следовательно, две прямые, перпендикулярные к третьей, не пересекаются. Что и требовалось доказать.

Теорема 2
Первый признак равенства треугольников ( по двум сторонам и углу между ними)

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.


Доказательство:

Так как ∠A=∠A1, то можно треугольник A1B1C1 наложить на треугольник ABC так, чтобы
точка A1 совместилась с точкой A,
луч A1C1 наложился на луч AC,
луч A1B1 — на луч AB.
Так как AB=A1B1, то при таком наложении сторона A1B1 совместится со стороной AB, а значит, точка B1 совместится с точкой B.
Аналогично, сторона A1C1 совместится со стороной AC, а точка C1 — с точкой C.
Следовательно, сторона B1C1 совместится со стороной BC.
Значит, при наложении треугольники полностью совместятся, поэтому ΔABC= ΔA1B1C1 (по определению).
Что и требовалось доказать.

Теорема 3
Теорема единственности перпендикуляра, проведенного из произвольной точки к заданной прямой
Из любой точки А, не лежащей на данной прямой, можно провести перпендикуляр к прямой. К тому же этот перпендикуляр единственный.

Дано: точка А не принадлежит прямой a.

Доказать: существует единственный отрезок АН, где АН- перпендикуляр к a из точки A.

1. Построим 2 равных угла. ∠АВС =∠МВС или ∠1 = ∠2.

2. Равные углы можно совместить наложением. При этом точка А перейдет в точку A1. ВА = ВA1(перегибание по прямой ВС).

3. Соединим точки А и A1. Получим точку Н. Углы ∠ВНА = ∠3, ∠ВНA1 = ∠4.

4. Так как ∠1 = ∠2,ВА = ВA1, BC- общая,то треугольники ВНА = ВНA1 по первому признаку равенства треугольников, то есть по углу и двум прилежащим сторонам. Из равенства треугольников следует равенство всех элементов. А значит, ∠3 = ∠4. Эти углы лежат против равных сторон. Два смежных равны только в случае, если каждый из них равен по 90°. А значит, АН ⊥ ВС. Мы доказали, что из точки А можно провести перпендикуляр к прямой a.

5. Предположим, что из точки А можно провести к прямой a два разных перпендикуляра.

Это невозможно, поскольку из разных точек прямой a проведены 2 перпендикуляра, которые имеют общую точку А. Мы получили противоречие, значит, наше предположение неверно. Из точки А можно провести лишь один перпендикуляр к прямой a. Теорема доказана.

Углом называется геометрическая фигура (рис. 1), образованная двумя лучами, исходящими из одной точки.
Точка О — вершина угла, а лучи ОА и ОБ — стороны угла. Обозначение: ∠AOB или ∠ab.
Угол в 90° называется прямым (рис. 2).
Угол, меньший прямого, называется острым (рис. 3).
Угол, больший прямого, но меньший развернутого, называется тупым (рис. 4).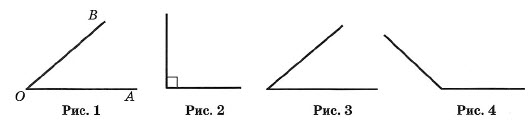


Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого (рис. 5).
∠AOC и ∠DOB; ∠BOC и ∠AOD — вертикальные.
Вертикальные углы равны: ∠AOC = ∠DOB и ∠BOC = ∠AOD.
Два угла называются смежными, если у них одна сторона общая, а две другие составляют прямую линию (рис. 6), ∠AOC и ∠BOC — смежные.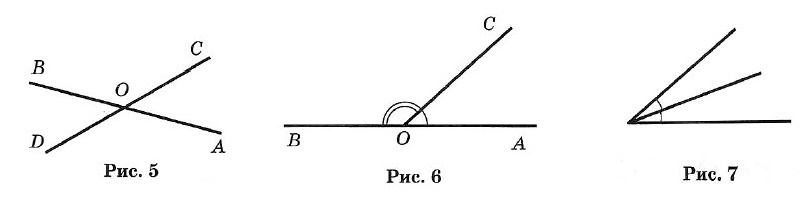


Сумма смежных углов равна 180°.
Биссектрисой угла называется луч, проходящий между сторонами угла и делящий его пополам (рис. 7).
Биссектрисы вертикальных углов составляют продолжение друг друга (рис. 8).
Биссектрисы смежных углов взаимно перпендикулярны (рис. 9).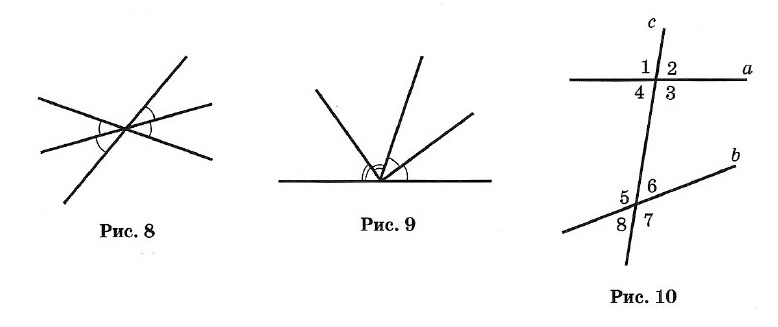


При пересечении двух прямых a и b третьей с (секущей) образуется 8 углов (рис. 10):
соответственные углы: ∠1 и ∠5, ∠2 и ∠6, ∠4 и ∠8, ∠3 и ∠7;
внутренние накрест лежащие: ∠4 и ∠6, ∠3 и ∠5;
внешние накрест лежащие: ∠1 и ∠7, ∠2 и ∠8;
внутренние односторонние: ∠4 и ∠5, ∠3 и ∠6;
внешние односторонние: ∠1 и ∠8, ∠2 и ∠7.

ABCDE — пятиугольник (рис. 11). Точки А, В, С, D, Е — вершины многоугольника; ∠A, ∠B, ∠C, ∠D, ∠E — углы; АВ, ВС, CD и т. д. — стороны; отрезки АС, AD, BE, BD, СЕ — диагонали; Р = АВ + ВС + … + ЕА — периметр многоугольника.
Многоугольник называется выпуклым (см. рис. 11), если он целиком расположен по одну сторону от каждой прямой, проходящей через две его соседние вершины. В противном случае многоугольник называется невыпуклым (рис. 12).


Свойства
1. Сумма внутренних углов произвольного n-угольника равна 180° • (n — 2).
2. Сумма внешних углов выпуклого n-угольника, взятых по одному при каждой вершине, равна 360°.
3. В выпуклом n-угольнике из каждой вершины можно провести (n — 3) диагоналей, которые разбивают n-угольник на (n — 2) треугольников.
4. В выпуклом n-угольнике число диагоналей равно n(n — 3)/2.

Выпуклый многоугольник, у которого равны все углы и стороны, называется правильным.
Свойства
1. Каждый угол правильного n-угольника равен а_n = 180°(n — 2)/n
2. Около правильного n-угольника можно описать окружность, и притом только одну.
3. В правильный n-угольник можно вписать окружность, и притом только одну.
4. Окружность, вписанная в правильный n-угольник, касается всех сторон n-угольника в их серединах.
5. Центр окружности, описанной около правильного n-угольника, совпадает с центром окружности, вписанной в тот же n-угольник.
6. Длина стороны правильного n-угольника, вписанного в окружность радиуса R, равна а = 2R sin(180°/n).
7. Длина стороны правильного n-угольника, описанного около окружности радиуса r, равна а = 2r tg(180°/n).

Треугольником называется геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, последовательно соединяющих эти точки.
Точки А, В, С — вершины треугольника АВС.
Отрезки АВ, ВС и АС — стороны, ∠A, ∠B и ∠C — углы. ∠A + ∠B + ∠C = 180°.
Стороны треугольника часто обозначают малыми буквами (рис. 13): АВ = с, ВС = а, АС = b.
Р = а + b + с — периметр треугольника.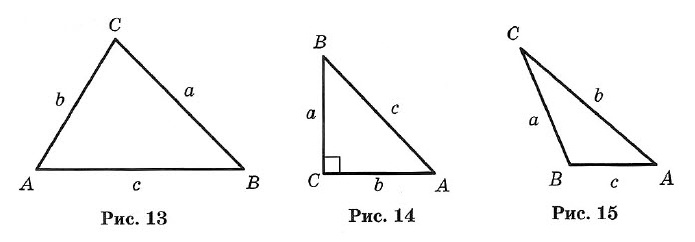


Треугольник, у которого все углы острые, называется остроугольным (см. рис. 13).
Треугольник, у которого есть прямой угол, называется прямоугольным (рис. 14).
Стороны, образующие прямой угол, называются катетами (а и b), а сторона, лежащая против прямого угла, — гипотенузой (с).
Треугольник с тупым углом называется тупоугольным (рис. 15).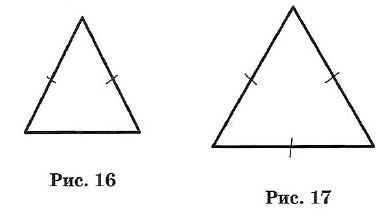


Треугольник, у которого две стороны равны, называется равнобедренным (рис. 16).
Равные стороны называются боковыми, а третья сторона — основанием равнобедренного треугольника.
Треугольник, у которого все стороны равны, называется равносторонним (рис. 17).
Каждый угол равностороннего треугольника равен 60°.

Свойства равнобедренного треугольника
1. Углы при основании равны.
2. Биссектриса, проведенная к основанию, является одновременно медианой и высотой.
3. Высота, проведенная к основанию, является одновременно медианой и биссектрисой.
4. Медиана, проведенная к основанию, является одновременно высотой и биссектрисой.


Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника (рис. 18). ∠CBD — внешний угол треугольника.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним (см. рис. 18): ∠CBD = ∠A + ∠C.
Отрезок, соединяющий середины двух сторон, называется средней линией треугольника (рис. 19).

I признак (признак равенства по двум сторонам и углу между ними).
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис. 20). АВ = А₁В₁, АС = А₁С₁, ∠A = ∠A₁

II признак (признак равенства по стороне и прилежащим к ней углам).
Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 21). АВ = A₁B₁, ∠A = ∠A₁, ∠B = ∠B₁

III признак (признак равенства пo трем сторонам).
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны (рис. 22). АВ = А₁В₁, ВС = B₁C₁, АС =А₁С₁.

Каждая сторона треугольника меньше суммы двух других сторон: а 2 2 + b 2 , то треугольник остроугольный;
б) если с 2 > а 2 + b 2 , то треугольник тупоугольный;
в) если с 2 = а 2 + b 2 , то треугольник прямоугольный.

1. Сумма острых углов равна 90° (рис. 23). ∠A + ∠B = 90°.
2. Катет, лежащий против угла в 30°, равен половине гипотенузы (рис. 24). a = c/2
3. Если катет равен половине гипотенузы, то угол, лежащий против этого катета, равен 30° (рис. 24).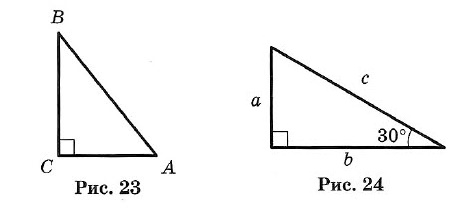

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны (рис. 25). АС = А₁С₁, ВС = В₁С₁.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого, то такие треугольники равны (рис. 26). АС = А₁С₁, ∠A = ∠A₁.


3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны (рис. 27). АВ = А₁В₁, ∠A = ∠A₁.
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны (рис. 28). АВ = А₁В₁, АС = А₁С₁

С каждым треугольником связаны 4 точки:
1) точка пересечения медиан;
2) точка пересечения биссектрис;
3) точка пересечения высот (или их продолжений);
4) точка пересечения серединных перпендикуляров к сторонам.
Эти четыре точки называются замечательными точками треугольника.
Высотой треугольника называется длина перпендикуляра, опущенного из любой его вершины на противолежащую сторону или ее продолжение.


В тупоугольном треугольнике (рис. 29) две высоты падают на продолжение сторон и лежат вне треугольника, а третья внутри.
В остроугольном треугольнике (рис. 30) все три высоты лежат внутри треугольника.
В прямоугольном треугольнике катеты одновременно служат и высотами (рис. 31).
Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром. В тупоугольном треугольнике ортоцентр лежит вне треугольника. В прямоугольном треугольнике он совпадает с вершиной прямого угла.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.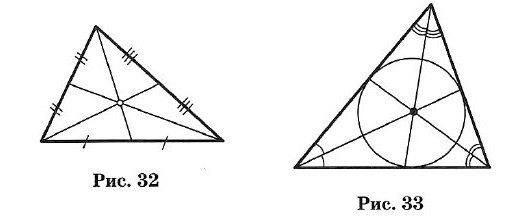


Три медианы треугольника пересекаются в одной точке, которая является центром тяжести треугольника (рис. 32).
Эта точка делит каждую медиану в отношении 2 :1 (считая от соответствующей вершины).
Биссектрисой треугольника называется отрезок биссектрисы угла от вершины до пересечения с противолежащей стороной.
Три биссектрисы треугольника пересекаются в одной точке, которая является центром вписанного круга (рис. 33).
Три перпендикуляра к сторонам треугольника, проведенные через их середины (рис. 34, 35, 36), пересекаются в одной точке, которая является центром описанной окружности.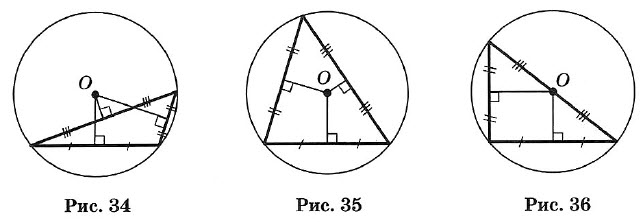


В тупоугольном треугольнике (рис. 34) эта точка лежит вне треугольника, в остроугольном (рис. 35) — внутри, в прямоугольном — на середине гипотенузы (рис. 36).
Ортоцентр, центр тяжести, центр вписанной и описанной окружностей совпадают друг с другом только в равностороннем треугольнике.

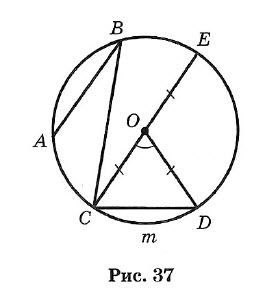
Окружностью называется геометрическое место точек плоскости, равноудаленных от одной ее точки (центра) (рис. 37).
Отрезок, соединяющий центр окружности с точкой на окружности, называется радиусом. Обозначение: г или R.
На рисунке ОС = ОЕ = OD = R.
Часть окружности (например, CmD) называется дугой.
Отрезок, соединяющий две точки окружности, называется хордой, а хорда, проходящая через центр, — диаметром.
АВ, ВС, CD и СЕ — хорды окружности. СЕ — наибольшая из хорд — диаметр. Обозначение: d или D.
D = 2R.
Часть плоскости, ограниченная окружностью, называется кругом.
Часть круга, ограниченная дугой (CmD) и стягивающей ее хордой (CD), называется сегментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Угол, образованный двумя радиусами, называется центральным (∠COD на рис. 37).
Угол, у которого вершина лежит на окружности, а стороны являются хордами, называется вписанным (например, ∠ABC).

Угол, образованный двумя касательными (СА и СВ), исходящими из одной точки, называется описанным (∠ACB на рис. 38).
1. Радиус, проведенный в точку касания, перпендикулярен касательной.
2. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.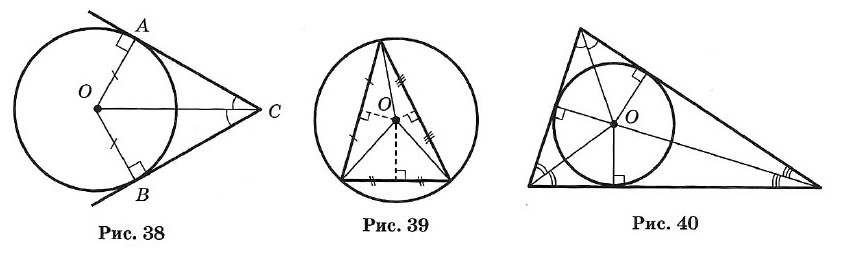

1. Около всякого треугольника можно описать окружность; центром окружности является точка пересечения перпендикуляров, проведенных к сторонам через их середины (рис. 39).
2. Во всякий треугольник можно вписать окружность; центром окружности является точка пересечения биссектрис (рис. 40).

Бывшая учительница математики предложила решение задачи о трисекции угла и просит найти ошибку

UPD от модерации: в комментариях имеются многочисленные свидетельства о явной ошибке

В челябинскую редакцию "РГ" обратилась читательница из Миасса с очень необычной проблемой. Пенсионерка, в прошлом учительница математики, Ляля Зарипова все свободное время посвящает любимому предмету и пытается решить еще не решенные задачи - по ее собственному выражению, стереть белые пятна, существующие в математике с древних времен. Однако, сумев найти решение одной из таких задач, она уже более двух лет безуспешно старается привлечь к нему внимание общественности.

Вопреки вердикту

Одна из старейших математических загадок, доставшаяся человечеству от грека Архимеда, получила название задачи о трисекции угла. Великий мыслитель и один из отцов геометрии попытался разделить угол на три равные части с помощью циркуля и линейки. Однако найти решение не смог и завещал эту загадку ученикам и потомкам.

Отметим, что любой школьник сегодня легко разделит угол на две половины. Линейки и циркуля для этого вполне достаточно. Без особого труда можно разбить на три равные части прямой угол, встроив в него равносторонний треугольник. Автор этих строк справился с задачкой, потратив не более пяти минут. Однако разделить любой угол на три равные части ученые до сих пор не смогли.

Еще в 1736 году известный французский математик Пьер Ванцель, проигнорировав условия Архимеда о циркуле и линейке, попытался найти "трисекцию угла" алгебраическим путем и… потерпел фиаско. В дальнейшем решение искать просто перестали. А в 1756-м Французская академия наук вынесла официальный вердикт о том, что эту задачу решить невозможно, и исключила ее из всех учебников и справочников того времени.

С тех пор о головоломке, некогда занимавшей лучшие математические умы, забыли. Ляля Гиззатовна искала "ключ" несколько лет и, перепробовав множество путей, нашла простое и блестящее решение, к которому, судя по оставшимся в истории записям, шел сам Архимед, но довести его до конца не сумел.

По мнению учительницы, чтобы разделить угол на три равные части, нужно провести из его основания окружность, отложить за ее пределами еще один радиус на биссектрисе, делящей этот угол пополам, и получить так называемый внешний угол. Он и будет в три раза меньше заданного угла, то есть станет одной из трех секций из условия задачи.

Последние три сотни лет решение даже не искали, а все это время математика шла семимильными шагами. Возможно, стоит попробовать снова?

Более того, автор геометрического подхода уверена: откладывая на биссектрисе нужное число радиусов, угол можно разделить не только на три, но и на пять, семь и девять частей - другими словами, разделить его на любое нечетное число. А это, в свою очередь, позволит найти решение еще одной математической головоломки - вписать в окружность любой правильный многоугольник. В справочниках до сих пор утверждается, что вписать правильные многоугольники, имеющие семь и девять сторон, в окружность невозможно. Ну разве это не открытие?

Однако, прежде чем понять, что решение единственно верное, Ляле Гиззатовне нужно было найти для него теоретическое обоснование. Для этого она сформулировала и доказала три теоремы, подтверждающие правильность подхода. И только после этого поделилась с миром своим открытием.

Хождение по академиям

- Однако рассказать о нем оказалось сложнее, чем сделать, - посетовала Ляля Гиззатовна. - С января 2018 года звонила, писала, умоляя чиновников от науки об одном - выслушайте! Но наталкивалась на глухую стену непонимания. Письма нераспечатанными возвращали назад. В телефонных переговорах после слов о том, что мне удалось найти трисекцию угла, обещали перезвонить и не перезванивали. Вероятно, принимали за сумасшедшую. Ведь во всех учебниках написано, что решения у этой задачи нет…

Сначала учительница обратилась в Минобрнауки РФ, однако оттуда ее перенаправили в Российскую академию наук. В РАН сослались на реорганизацию и попросили написать в математический институт имени В.А. Стеклова, где объяснили, что занимаются высшей математикой, а вопросы, касающиеся элементарной математики, - компетенция специально созданного института по работе с научными открытиями.

- Директор этого учреждения, услышав голос "очередного изобретателя вечного двигателя", посоветовал получше изучить геометрию, в которой черным по белому записано, что задача о трисекции угла не имеет решения. А когда я начала его убеждать, посоветовал сначала опубликовать работу в каком-нибудь научном издании, а уж потом отнимать время у академиков, - вспоминает этот разговор учительница.

Дальше была переписка с Казанским и Новосибирским отделениями РАН, откуда Ляля Гиззатовна получила выдержку из Википедии. В итоге письмо учительницы вернулось обратно в Минобрнауки РФ, и круг замкнулся…

Чтобы помочь Ляле Гиззатовне донести свои мысли до широкой общественности, предлагаем ей прямо в редакции вооружиться циркулем и линейкой. Снимаем на видео, как она делит угол на три равные части, а затем договариваемся о встрече с известным челябинским ученым, академиком РАН Сергеем Матвеевым и его коллегами-математиками из Челябинского госуниверситета.

Сначала предложение посмотреть видео с решением задачи о трисекции угла встречает тот же отпор, с которым в течение двух лет сталкивалась педагог.

- Этой проблемой занималось не одно поколение математиков, - возмущается Сергей Матвеев. - Какое бы решение ни предложили, оно однозначно неверное. Иначе это действительно сенсация, и с ней можно претендовать на Нобелевскую премию.

- Но ведь, если верить истории, последние три сотни лет решение даже не искали, а все это время математика шла семимильными шагами, - пытаемся привести аргумент Ляли Гиззатовны.

- Возможно, стоит попробовать снова? Ведь в XVIII веке могли и ошибаться?

- Мир остался прежним, как и его законы, - отметает довод доцент кафедры математики Филипп Кораблев. - Если вы бросите камень, он на Марс не улетит. Мы, конечно, можем посмотреть видео и, возможно, даже не обнаружим в этом решении ошибку, но она там обязательно есть. Мы бы посоветовали учительнице поискать ее самой!

Вот как! И это экспертное мнение? Проявив немалую настойчивость, нам все-таки удается уговорить математиков потратить пять-семь минут на видео. Несмотря на высказанное недоверие, происходящее на экране вызывает у них неподдельный интерес.

Сотрудники кафедры поэтапно перематывают ролик и ищут "вкравшуюся" ошибку, обмениваясь оживленными репликами: "Если решение строится на том, что это ромб, то оно неверно, поскольку две его вершины находятся на окружности", "А действительно ли эти хорды проходят через центр окружности? Видите, как дрогнула рука, когда она их чертила?".

И, хотя явной ошибки, подрывающей все математические устои, как и предупреждал Филипп Кораблев, с ходу найти не удается, они остаются при своем мнении: решение не может быть правильным, потому что доказано обратное! Именно эту мысль и попросил как можно деликатнее донести до Ляли Гиззатовны Сергей Матвеев. А потом добавил:

- А вообще… Было интересно…

Отложите гаджеты

Рассказывая о невозможности решить задачу Архимеда, доцент Кораблев вспомнил, как в школе ее предложила учительница математики - видимо, просто устала от класса:

- Мы пол-урока ломали головы и выдвигали свои версии, конечно, изначально неверные. И только после узнали, что она просто пошутила и водила нас за нос.

Но ведь как минимум один человек из этого класса все-таки стал математиком, разве не так?

Сегодня увлечь детей настолько, чтобы они хотя бы на пять минут отложили в сторону любимые гаджеты, - задачка не из простых. И не всякая школа способна ее решить. Интерес к естественным наукам, физике и математике, царивший в эру завоевания космоса, сильно упал. И пробудить его могли бы подвижники-учителя, такие как Архимед, преподаватель математики доцента Кораблева или скромная пенсионерка из Миасса Ляля Зарипова.

Энергии и увлеченности этого человека можно позавидовать. В 86 лет Ляля Гиззатовна продолжает увлекать любимым предметом окружающих. Наверное, поэтому к ней по-прежнему обращаются с просьбой подтянуть детей по математике. Ведь после ее уроков ученик начинает стараться понять, а не зазубрить, решить, а не списать из Интернета…

Возможно, Ляля Гиззатовна и правда достойна Нобелевской премии? "РГ" обращается ко всем, кто силен в математике и геометрии: давайте найдем ошибку в решении, предложенном учительницей. А может, никакой ошибки нет? Решив задачу о трисекции угла, Ляля Гиззатовна пытается разгадать загадку простых натуральных чисел…