Разложение функций в степенные ряды шпора

Продолжаем рассматривать теорию и практику степенных рядов. Материал несложный, но для его понимания необходимо уже более или менее хорошо ориентировать в теме. Если Вы только-только приступили к изучению рядов или чувствуйте себя чайником, пожалуйста, начните с урока Ряды для чайников. Примеры решений. Далее следует прочитать статью Степенные ряды. Область сходимости ряда, в частности, Вы должны хорошо понимать, что такое степенной ряд и его область сходимости. А для целей сегодняшнего урока потребуется методический материал Таблица разложений некоторых функций в степенные ряды, его можно раздобыть в кладовке Математические формулы и таблицы. По возможности, таблицу лучше распечатать, поскольку она потребуется не только сейчас, но и в оффлайне.

Понятие суммы степенного ряда

Чтобы всё стало окончательно понятно, рассмотрим примеры с картинками. Я выпишу простейшее табличное разложение синуса в степенной ряд:

(По какому принципу получены сами элементарные табличные разложения, мы рассмотрим чуть позже).

Вот такая симпатичная синусоида. Хмм…. Где-то я уже это видел….

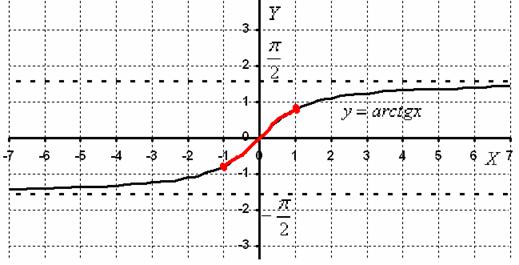
Исходя из вышесказанного, можно сформулировать две взаимно обратные задачи:

– найти сумму ряда (функцию) по известному разложению;
– разложить функцию в ряд (если это возможно) и найти область сходимости ряда.

Что проще? Конечно же, разложение – с него и начнём. После чего я рекомендую не затягивать и в ближайшие часы-дни (пока свежи воспоминания) потренироваться в нахождении суммы степенного ряда.

Разложение функций в степенной ряд.
Ряд Тейлора. Ряд Маклорена

Приступим к увлекательному занятию – разложению различных функций в степенные ряды. Сначала пара формул, затем практические задания.

Данная формула носит фамилию англичанина Тейлора (ударение на первый слог).

Подставляем единицы в формулу Маклорена и получаем наше табличное разложение!

Аналогично можно вывести некоторые другие табличные разложения (но далеко не все выводятся именно так).

Примеры разложения функций в ряд Маклорена

В данном параграфе мы рассмотрим типовую задачу на разложение функции в ряд Маклорена и определении области сходимости полученного ряда. Нет, мучаться с нахождением производных не придется, мы будем пользоваться таблицей.

Разложить функцию в ряд Маклорена. Найти область сходимости полученного ряда.

Решение незамысловато, главное, быть внимательным.

Конструируем наш ряд. Плясать начинают, как правило, от функции, разложение которой есть в таблице:

Это пример для самостоятельного решения.

А сейчас для разнообразия рассмотрим что-нибудь с минусами.

Но так бывает далеко не всегда:

Интересно отметить, что разложение в ряд такого логарифма:

Таким образом, с логарифмами нужно работать осмотрительно!

Пара примеров для самостоятельного решения:

Здесь разложение не такое сложное, но могут возникнуть трудности с нахождением области сходимости полученного ряда.

Полные решения и ответы в конце урока.

Это пример для самостоятельного решения.

Разложение функций в ряд Маклорена необходимо проводить и в ряде других задач, например, в задаче приближенного вычисления определенного интеграла. Кстати, там, помимо нового материала, можно посмотреть примеры других разложений, которые не поместились в этот урок.

Данное задание является более сложным и встречается значительно реже, но всё-таки 2-3 примера не помешают. Пригодится.

Вытащим из чулана общую формулу Тейлора:

Очень хорошо если вы проработали урок Производные высших порядков, впрочем, я постараюсь максимально подробно закомментировать оставшиеся задачи.

И сразу небольшой Пример 8

Теперь подставляем весь найденный скарб в формулу Тейлора:

Рассмотрим более содержательные примеры.

Хех, опять предстоит ручная работа….

Замечаем, что с такими раскладами производные можно находить до бесконечности. Поэтому необходимо уловить некоторую закономерность. Найдем ещё третью производную:

А теперь проанализируем найденные производные:

Закономерность прослеживается: знаки чередуются, в числителе накручивается факториал, а в знаменателе растёт степень.

Возникает вопрос: а зачем тогда возиться с производными? И ответ здесь такой: замена далеко не всегда приводит к желаемому результату, так, например, она совершенно бесполезна в Примере 8, и ещё много для каких функций. Поэтому главным и основополагающим методом следует считать прямое построение ряда через производные.

Заключительный пример для самостоятельного решения:

В образце приведены оба способа решения.

Как ваш тонус? Я так и знал, что на высоте! – поэтому самое время потренироваться в нахождении сумм степенных рядов по известным разложениям. Кроме того, на следующем уроке много интересной и. неожиданной информации. Только не злоупотребляйте =)

Решения и ответы:

(Переход на главную страницу)

Лекции 33,34. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд (4ч)

Ряды Тейлора и Маклорена. Разложение функции в степенной ряд, необходимое, достаточные условия. Приложения степенных рядов. Примеры.

Разложение в ряд Маклорена некоторых элементарных функций. Приближенное вычисление значений функции с помощью степенных рядов.

Ряд Тейлора и Маклорена

то говорят, что функция f(x) разлагается в степенной ряд в окрестности точке х₀ ( или в ряд по степеням х – х₀ ).

Теорема 2.

Доказательство. Пусть в окрестности х₀ справедливо разложение

f(x) = а₀ + а₁(х – х₀) + а₂(х – х₀) 2 + а₃(х – х₀) 3 + а₄(х – х₀) 4 + . (3)

Положим в этом равенстве х = х₀, получим а₀ = f(x₀) .

Так как ряд в окрестности х₀ сходится, то его можно дифференцировать. Продифференцируем равенство (3) п раз, получим

f¢ (x) = а₁ +2а₂(х – х₀) + 3а₃(х – х₀) 2 + 4а₄(х – х₀) 3 +.

f¢¢ (x) = 2а₂+ 6а₃(х – х₀) +12 а₄(х – х₀) 2 + .

f¢¢¢ (x) = 6а₃+ 24а₄(х – х₀) + .

f (п) (x) = п(п–1)(п–2). 2а_п + (п+1)п(п–1). 2 а_п₊₁(х – х₀) +.

Полагая в этих равенствах х = х₀, получим

Из теоремы 7.2. следует:

1) если функция f(x) разлагается в степенной ряд в окрестности точки х₀, то это есть обязательно ряд Тейлора этой функции:

2) Если функция f(x) разложима в степенной ряд в окрестности точки х₀, то она бесконечное число раз дифференцируема в этой окрестности (это свойство называют необходимым условием разложимости в степенной ряд).

Теорема 7.2. формулирует необходимое, но не достаточное условие разложимости функции в степенной ряд. Т.е. нельзя утверждать, что ряд Тейлора, формально составленный для функции f(x) , сходится обязательно к этой функции.

Достаточные условия сходимости ряда Тейлора к самой функции (т.е. разложимости функции в степенной ряд) дает следующая

Теорема 3.

Для того чтобы функция f(x) могла быть разложена в степенной ряд (ряд Тейлора) в окрестности U(x₀) точки х₀, необходимо и достаточно, чтобы остаток этого ряда стремился к нулю при п ®¥ "х из этой окрестности , т.е.

для всех хÎU(x₀).

При этом исследование поведения остатка ряда удобно проводить, используя различные формы записи остатка ряда, в частности форму Лагранжа:

где x – некоторое число, удовлетворяющее условию 0 (п) (x) ) и вычислить их значения в точке х₀.

2. Записать формально ряд Тейлора для f(x) .

3. Найти область сходимости этого ряда.

Пример 1. Разложим функцию е х в ряд в окрестности точки х = 0 (ряд Тейлора с центром в точке х = 0 называется рядом Маклорена). Будем пользоваться сформулированным алгоритмом.

1. Очевидно, f (п) (x) = е х , тогда f (п) (0) = 1

4. Изучим поведение остатка ряда. Запишем остаток ряда в форме Лагранжа:

Пример 2. Разложим в ряд Маклорена функцию f(x) = sin x. Имеем:

f(x) = sin x, f(0) = 0

f¢¢(x) = –sin x = sin (x + p ), f ¢¢(0) = 0

f IV (x) = sin x = sin (x + 2p ), f IV (0) = 0,

Тогда ряд Тейлора имеет вид

Найдем область сходимости этого ряда:

Проинтегрировав последнее равенство, получим

Заметим, что в граничных точках полученный ряд сходится условно:

Пользуясь вышеописанным алгоритмом можно получить следующее разложение

Таким образом, мы имеем перечень известных разложений:

Понятие степенного ряда, его сходимость и расходимость

Среди функциональных рядов наиболее важное место занимают степенные ряды.

Степенным рядом называют ряд

члены которого – степенные функции, расположенные по возрастающим целым неотрицательным степеням x , а c 0 , c 1 , c 2 , c n - постоянные величины. Числа c 1 , c 2 , c n - коэффициенты членов ряда, c 0 - свободный член. Члены степенного ряда определены на всей числовой прямой.

Вместо x могут быть различные числа.

При некоторых значениях x степенные ряды могут быть сходящимися, при других значениях x - расходящимися. Обозначим через x 0 некоторое значение x , при котором ряд сходится, а через x 1 - значение, при котором ряд расходится. На рисунке слева показано, что интервал от −x 0 до x 0 является интервалом сходимости ряда, а вне этого интервала наблюдается расходимость.

Но как определить эти граничные значения x ? Для этого существует вполне определённый способ. Обозначим эти граничные значения через −R и R . Находим по следующей формуле:

А теперь всё это в более точных формулировках, после чего перейдём к решению задач.

Область сходимости, интервал сходимость и радиус сходимости степенного ряда

Множество значений переменной x , для которых ряд сходится, называется областью сходимости степенного ряда.. Для действительных значений переменной x область сходимости состоит либо из одной точки, либо является некоторым интервалом (интервалом сходимости), либо совпадает со всей осью Ox.

При подстановке в степенной ряд значения x=0 получится числовой ряд

Следовательно, при x=0 сходится любой степенной ряд и, значит, область его сходимости не может быть пустым множеством. Есть степенные ряды, которые сходятся только при x=0 и расходятся при остальных значениях х. Структура области сходимости всех степенных рядов одинакова. Её можно установить с помощью следующей теоремы, которая уже была проиллюстрирована в начале этого урока.

Теорема 1 (теорема Абеля). Если степенной ряд сходится при некотором значении x = x 0 , отличном от нуля, то он сходится, и притом абсолютно, при всех значениях |x| 0 | . Обратите внимание: и отправное значение "икс нулевое" и любое значение "икса", которое сравнивается с отправным, взяты по модулю - без учёта знака.

Следствие. Если степенной ряд расходится при некотором значении x = x 1 , то он расходится и при всех значениях |x| > |x 1 | .

Пример 1. Найти область сходимости степенного ряда

Используя формулу (28), найдём радиус сходимости данного ряда:

Пример 2. Найти область сходимости степенного ряда

Решение. Коэффициенты ряда положительны, причём

Найдём предел этого отношения, то есть радиус сходимости степенного ряда:

Пример 3. Найти область сходимости степенного ряда

По формуле (28) находим радиус сходимости ряда:

Пример 4. Найти область сходимости степенного ряда

Следовательно, радиус сходимости ряда

Пример 5. Найти область сходимости степенного ряда

Согласно формуле (28) радиус сходимости данного ряда

то есть ряд сходится только при x=0 и расходится при остальных значениях х .

Примеры показывают, что на концах интервала сходимости ряды ведут себя различно.

Формула радиуса сходимости степенного ряда получена в предположении, что все коэффициенты членов ряда, начиная с некоторого, отличны от нуля. Поэтому применение формулы (28) допустимо только в этих случаях. Если это условие нарушается, то радиус сходимости степенного ряда следует искать с помощью признака Даламбера, или же, сделав замену переменной, преобразованием ряда к виду, в котором указанное условие выполняется.

Пример 6. Найти интервал сходимости степенного ряда

Сумма степенного ряда. Дифференцирование и интегрирование степенных рядов

Пусть для степенного ряда

Тогда каждому значению х из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначая её через f(x), можем записать равенство

понимая его в том смысле, что сумма ряда в каждой точке х из интервала сходимости равна значению функции f(x) в этой точке. В этом же смысле будем говорить, что степенной ряд (29) сходится к функции f(x) на интервале сходимости.

Вне интервала сходимости равенство (30) не имеет смысла.

Пример 7. Найти сумму сумму степенного ряда

Приведем теоремы о почленном дифференцировании и интегрировании степенных рядов.

Разложение функций в степенные ряды

Пусть дана функция f(x), которую требуется разложить в степенной ряд, т.е. представить в виде (30):

Полагая в равенствах (30) и (31) х = 0, находим

Подставляя найденные выражения в равенство (30), получим

Это разложение функции f(x) в ряд называется рядом Маклорена.

Найдём разложение в ряд Маклорена некоторых элементарных функций.

Решение. Производные этой функции совпадают с самой функцией:

Поэтому при х=0 получаем

Подставляя эти значения в формулу (32), получим искомое разложение:

Пример 9. Разложить в ряд Маклорена функции: 1) f(x)=sinx ; 2) f(x)=cosx .

1)Находим производные функции f(x)=sinx ; имеем

Так как производная четвёртого порядка совпадает с функцией, то производные следующих порядков повторяются в той же последовательности. Найдём значения функции и её производных при х = 0:

Поэтому ряд Маклорена для f(x)=sinx имеет вид

производные следующих порядков повторяются в той же последовательности. Далее, имеем

В результате получаем следующее разложение функции f(x)=cosx в ряд Маклорена:

Пример 10. Разложить в ряд Маклорена функцию f(x) = sin²x .

Решение. Находим производные данной функции:

(при n ). Необходимо различать две возможности для показателя степени m . Если m – целое положительное число, то при n=m получим

т.е. постоянную величину, а потому производные следующих порядков равны нулю. Найдём значения функции и её производных при x=0 :

Подставляя эти значения в формулу (32), после упрощений получим

Это не ряд, а сумма, состоящая из конечного числа слагаемых и представляющая собой известное разложение бинома Ньютона.

Подстановка значений функции и её производных в равенство (32) в этом случае даёт

Полученный ряд называется биномиальным. Найдём его интервал сходимости. Так как коэффициенты этого ряда

то их отношение после упрощения принимает вид

Содержание

1 Степенные ряды
2 Примеры разложения функций
- 2.1 e^x
- 2.2 ln(1 + x)
- 2.3 n!. Формула Стирлинга
- 2.4 sin(x) и cos(x)
- 2.5 (1 + x)^a

Степенные ряды [ править ]

Пусть $ f(x) = \sum\limits_^ <\infty>a_n (x - x_0)^n, \qquad R > 0 \qquad (x_0 - R; x_0 + R) $.

В силу сказанного ранее, f - бесконечно дифференцируема, все производные записываются степенными рядами с тем же радиусом сходимости: $ f^<(p)>(x) = \sum\limits_^ <\infty>n (n - 1) \dots (n - p + 1) a_n (x - x_0)^$ $ \forall x $ из промежутка сходимости.

Подставим $ x = x_0 $:

$f^<(p)>(x_0) = p! \cdot a_p \Rightarrow a_p = \frac(x_0)> $

Пусть в $ x_0 $ задана $ y = f(x) $, в точке $ x_0 $ существуют производные любого порядка.

Определение:

$ \sum\limits_^ <\infty>\frac(x_0)> (x - x_0)^n $ - ряд Тейлора функции по степеням $ (x - x_0) $.

Сопоставим ряд с формулой Тейлора функции, которую можно писать для любого $ n $.

$ f(x) = \sum\limits_^ \frac(x_0)> (x - x_0)^k + r_n(x) \Rightarrow $ ряд получается из формулы при $ n \to \infty $. Если $ r_n(x) \rightarrow 0 $ при $ n \rightarrow \infty $, то можно перейти к пределу.

$ f(x) = \sum\limits_^ <\infty>\frac(x_0)> (x - x_0)^k $, что является разложением функции в степенной ряд в точке $ x $.

Если при всех x из некоторой окрестности точки $ x_0 $ функция разлагается в степенной ряд, то это будет обязательно ряд Тейлора.

Если разложение возможно, то единственно. Изучается с помощью поведения остатка $ r_n(x) $.

Приведем пример неразложимой в ряд Тейлора функции: $ f(x) = \begin0, x = 0\\e^<-\frac 1>, x \ne 0\end $

Можно убедиться, что все $ f^<(p)>(x) = 0 \Rightarrow $ ряд Тейлора по $ x = 0 $, хотя функция таковой не является.

Причина объясняется в поле $ \mathbb $.

Примеры разложения функций [ править ]

Приведем классические разложения, некоторые обоснуем.

Рассмотрим $ y = e^x; \qquad (e^x)^ <(p)>= e^x $

$ e^x = \sum\limits_^n \frac1 x^k + r_n(x); \qquad r_n(x) = \frac> <(n + 1)!>x^, \theta_n \in [0; 1] $

Покажем, что $ \forall x: r_n(x) \xrightarrow[]<> 0 $

Пусть $ x > 0 $ $ e^ <\theta_n x>\le e^x \Rightarrow |r_n(x)| \le e^x \frac> <(n + 1)!>\Rightarrow r_n(x) \to 0 $

Итого, $ e^x = \sum\limits_^ <\infty>\frac $ с радиусом сходимости $ +\infty $.

В связи с этими разложением Эйлер совершил революцию в умах.

$ e \stackrel <=>\lim\limits_ (1 + \frac1n)^n $

Внезапно, мы решили что $ \lim\limits_ (1 + x)^ <\frac1x>= e $

Эйлер поступил по-другому:

Рассмотрим ряд $ \sum\limits_^ <\infty>\frac1 x^n : \frac> = n + 1 \to +\infty \Rightarrow R = +\infty \Rightarrow $ у ряда есть сумма, которую обозначают $ f(x) $.

Далее, $ f(x), f(y) $ - перемножим степенные ряды по правилу Коши:

n-й член $ \sum\limits_^n \frac \frac> <(n - k)!>= \frac1 \sum\limits_^n C^k_n x^k y^ = \frac1 (x + y)^n $

$ f(x) f(y) = \sum\limits_^ <\infty>\frac1 (x + y)^n = f(x + y) $

$ (1 + \frac1n)^n \le \sum\limits_^n \frac1 $. С другой стороны, если часть слагаемых опустить, сумма уменьшится.

$ (1 + \frac1n)^n \ge \sum\limits_^N \frac1 (1 - \frac0n) (1 - \frac1n) \dots (1 - \fracn) $. Устремим [math]n[/math] к бесконечности. Так как число слагаемых в сумме и множителей в каждом слагаемом конечно, сделаем в сумме предельный переход:

$ e \ge \sum\limits_^N \frac1 $.

Итого: $ (1 + \frac1N)^N \le \sum\limits_^N \frac1 \le e $

Теперь устремим [math] N [/math] к бесконечности:

Итак, $ e \le \sum\limits_^ <\infty>\frac1 \le e \Rightarrow f(1) = e $

Рассмотрим $ f = ln(1 + x) $ и разложим ее в степенной ряд другим приемом.

$ (\ln(1 + x))' = \frac1 <1 + x>= \sum\limits_^ <\infty>(-1)^n x^n, |x| n!. Формула Стирлинга [ править ]

Установим классическую асимптотическую формулу Стирлинга для факториала:

|proof= Выше доказано, что $ \ln(1 + x) = x - \frac2 + \frac3 - \dots , \ln(1 - x) = -x - \frac2 - \frac3 - \dots $

Вычтем из первой формулы вторую: $ \ln(\frac<1 + x><1 - x>) = 2x + \frac<2x^3>3 + \frac<2x^5>5 + \dots $

$ x = \frac1 <2n + 1>$ - допустимо, $ |x| 1 $

С другой стороны,

$ 1 + \frac13 <\left( \frac1<2n + 1>\right)>^2 + \frac15 <\left( \frac1<2n + 1>\right)>^4 + \dots 1 \Rightarrow $ последовательность $ a_n $ убывает, значит, по теореме Вейерштрасса, $ \exists a = \lim\limits_ a_n $, $ a \le a_n $

$ b_n = a_n \cdot e^<- \frac1<12n>>, e^<- \frac1<12n>> \to 1 $ $ a_n \to a \Rightarrow b_n \to a $

Поступая аналогично, можно разложить тригонометрические функции sin и cos и обратить внимание на ограниченность $ \sin^ <(n)>(x) \Rightarrow r_n(x) \to 0 \quad \forall x $.

Окончательно установлена аналитическая природа тригонометрических функций.

Исходя из арифметических действий:

$ \sin^2(x) + \cos^2(x) = 1 $

$ \sin(x + y) = \sin(x) \cos(y) + \sin(y) \cos(x) $

Остаток по Коши формулы Тейлора(1 том, стр. 257):

$ r_n(x) = \frac (x_0 + \theta (x - x_0))> (1 - \theta)^n (x - x_0)^ $, где $ 0 1 $ - расходится.

Исследование $ r_n(x) $ будем проводить в форме Коши :

Так как $f^<(n + 1)>(x) = a (a - 1) \dots (a - n + 1) (a - n) (1 + x)^ $, то получим:

Перегруппируем множители, получим:

Первое из этих трех выражений представляет собой общий член биномиального ряда, но отвечающего показателю $ a - 1 $, так как при $ |x|

Лекции 33,34. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд (4ч)

Ряд Тейлора и Маклорена

то говорят, что функция f(x) разлагается в степенной ряд в окрестности точке х₀ ( или в ряд по степеням х – х₀ ).

Теорема 2.

Доказательство. Пусть в окрестности х₀ справедливо разложение

f(x) = а₀ + а₁(х – х₀) + а₂(х – х₀) 2 + а₃(х – х₀) 3 + а₄(х – х₀) 4 + . (3)

Положим в этом равенстве х = х₀, получим а₀ = f(x₀) .

f¢ (x) = а₁ +2а₂(х – х₀) + 3а₃(х – х₀) 2 + 4а₄(х – х₀) 3 +.

f¢¢ (x) = 2а₂+ 6а₃(х – х₀) +12 а₄(х – х₀) 2 + .

f¢¢¢ (x) = 6а₃+ 24а₄(х – х₀) + .

f (п) (x) = п(п–1)(п–2). 2а_п + (п+1)п(п–1). 2 а_п₊₁(х – х₀) +.

Полагая в этих равенствах х = х₀, получим

Из теоремы 7.2. следует:

Теорема 3.

для всех хÎU(x₀).

где x – некоторое число, удовлетворяющее условию 0 (п) (x) ) и вычислить их значения в точке х₀.

2. Записать формально ряд Тейлора для f(x) .

3. Найти область сходимости этого ряда.

1. Очевидно, f (п) (x) = е х , тогда f (п) (0) = 1

4. Изучим поведение остатка ряда. Запишем остаток ряда в форме Лагранжа:

Пример 2. Разложим в ряд Маклорена функцию f(x) = sin x. Имеем:

f(x) = sin x, f(0) = 0

f¢¢(x) = –sin x = sin (x + p ), f ¢¢(0) = 0

f IV (x) = sin x = sin (x + 2p ), f IV (0) = 0,

Тогда ряд Тейлора имеет вид

Найдем область сходимости этого ряда:

Проинтегрировав последнее равенство, получим

Заметим, что в граничных точках полученный ряд сходится условно:

Пользуясь вышеописанным алгоритмом можно получить следующее разложение

Таким образом, мы имеем перечень известных разложений:

Теорема Абеля

Область сходимости степенного ряда

Здесь возможны три случая:

1) Область сходимости состоит только из одной точки х=0, то есть ряд расходится для всех значений х, кроме х=0. Пример

2) Область сходимости состоит из всех точек оси ОХ, то есть ряд сходится при всех значениях х. Пример

Начиная с номера n, элементы ряда по абсолютной величине будут меньше элементов сходящейся геометрической прогрессии. Следовательно, при любом х ряд сходится.

3) Область сходимости состоит более чем из одной точки оси ОХ, причем есть точки оси, не принадлежащие области сходимости. Пример

Это геометрическая прогрессия со знаменателем х. Ряд сходится при |x| R ряд расходится. При x=R и x=-R различные варианты:

А) ряд сходится в обеих точках.

Б) ряд сходится в одной из точек.

В) ряд расходится в обеих точках.

Радиусом сходимости степенного ряда (*) называется такое число R, что для любых х, |x| R, расходится. Интервал (-R,R) называется интервалом сходимости.

Считаем, что если ряд расходится для любого х, кроме х=0, R=0.

Способ отыскания радиуса сходимости степенного ряда

Отметим, что для нахождения радиуса сходимости можно исследовать ряд, составленный из абсолютных величин элементов исходного ряда, то есть

Для тех значений х, при которых получаемый предел меньше 1, ряд сходится, а для тех, при которых x>1, ряд расходится. Отсюда следует, что значения |x|, при которых этот предел равен 1, и будет являться радиусом сходимости ряда.

Наоборот, если для любых х кроме х=0 предел равен бесконечности, то ряд будет везде расходиться, кроме х=0, то есть R=0.

Если |x| 1 – ряд расходится

При х=1 получаем гармонический ряд, который расходится.

При |x| 1 – ряд расходится

При |x|=1 – ряд сходится абсолютно.

Лемма 2

Степенной ряд, составленный из производных элементов ряда (*) имеет тот же радиус сходимости, что и данный ряд.

Доказательство

Равенство пределов отношения последующего элемента к предыдущему для обоих рядов, показывает, что их радиусы сходимости равны.

Следует отметить, что на конце интервала сходимости ряд (**) может расходиться и тогда, когда ряд (*) сходится.

Если теперь составить ряд из производных ряда (**), то он опять будет иметь тот же радиус сходимости и т.д. Таким образом, все степенные ряды, получающиеся последовательным дифференцированием ряда (*) имеют один и тот же радиус сходимости и по лемме 1 правильно сходятся в любом интервале, целиком принадлежащем интервалу сходимости.

Свойство 1

Сумма степенного ряда есть функция, непрерывная в интервале сходимости ряда:

Заметим, что в том конце интервала, где степенной ряд сходится, его сумма S(x) остается односторонне непрерывной (изнутри интервала сходимости).

Следует учитывать одно обстоятельство, которое может иногда привести к недоразумению.

Возьмем геометрическую прогрессию, сходящуюся при |x| 1 ряд расходится и о его сумме говорить нельзя.

Свойство 2

Степенной ряд можно поэлементно интегрировать в интервале сходимости

Свойство 3

Степенной ряд можно поэлементно дифференцировать в интервале сходимости

Итак, степенной ряд в интервале его сходимости можно поэлементно дифференцировать любое число раз, при этом радиусы сходимости получающихся рядов остаются прежними.

Разложение функции в степенные ряды

Известно, что сумма степенного ряда в интервале сходимости этого ряда является непрерывной и бесконечное число раз дифференцируемой.

Когда можно утверждать, что заданная функция f(x) является суммой некоторого степенного ряда?

Из свойств степенных рядов следует, что эта функция должна быть бесконечное число раз дифференцируема (но это условие не достаточное).

Остается вопрос установить, какие функции и в каких интервалах можно представить в виде суммы степенных рядов.

В дальнейшем, если заданную функцию f(x) можно представить в виде суммы некоторого степенного ряда, то говорят, что функция f(x) разложена в степенной ряд.

Важность такого разложения очевидна, так как, получаем возможность приближенно заменить функцию суммой нескольких первых элементов степенного ряда, то есть многочленом. Вычисление значений многочленов – простейшие арифметические операции. Важно, что можно оценить точность получаемых приближенных значений.

Замена функции таким простым выражением, как многочлен, оказывается очень удобной в различных вопросах мат. анализа: при вычислении интегралов, решении дифференциальных уравнений и т.д.

Определение

Замечание

Читайте также: