Продольная деформация закон гука шпора

Деформации при растяжении и сжатии

Характер деформаций, которым подвергается прямой брус при растяжении или сжатии мы определили, проведя опыт с резиновым брусом, на котором была нанесена сетка линий.
Теперь представим себе брус постоянного сечения имеющий длину l , один из концов которого защемлен, а к свободному концу приложена растягивающая сила F . Под действием этой силы брус удлинится на некоторую величину Δl , которую назовем абсолютным удлинением бруса .
Отношение абсолютного удлинения Δl к первоначальной длине бруса l назовем относительным удлинением и обозначим ε :

Относительное удлинение – величина безразмерная, иногда его выражают в процентах.

Итак, деформация бруса при растяжении и сжатии характеризуется абсолютным и относительным удлинением или укорочением.

Напряжения и деформации при растяжении и сжатии связаны между собой линейной зависимостью, которая называется законом Гука, по имени английского физика Р. Гука (1653-1703 г.г.), установившего этот закон.
Сформулировать закон Гука можно так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению .

Математически эта зависимость записывается так:

Здесь Е – коэффициент пропорциональности, который характеризует жесткость материала бруса, т. е. его способность сопротивляться деформации; его называют модулем продольной упругости , или модулем упругости первого рода .
Модуль упругости, как и напряжение, выражаются в паскалях (Па) .

Значения Е для различных материалов устанавливаются экспериментально-опытным путем, и их величину можно найти в соответствующих справочниках.
Так, для стали Е = (1,96.…2,16) х 10 5 МПа, для меди Е = (1,00. 1,30) х 10 5 МПа и т. д.

Следует оговориться, что закон Гука справедлив лишь в определенных пределах нагружения.
Если в формулу закона Гука подставить полученные ранее значения относительного удлинения и напряжения: ε = Δl / l , σ = N / А , то можно получить следующую зависимость:

Произведение модуля упругости на площадь сечения Е×А , стоящее в знаменателе, называют жесткостью сечения при растяжении и сжатии; оно характеризует одновременно и физико-механические свойства материала бруса и геометрические размеры поперечного сечения этого бруса.

Приведенную выше формулу можно читать так: абсолютное удлинение или укорочение бруса прямо пропорционально продольной силе и длине бруса, и обратно пропорционально жесткости сечения бруса.
Выражение ЕА / l называют жесткостью бруса при растяжении и сжатии .

Приведенные выше формулы закона Гука справедливы лишь для брусьев и их участков, имеющих постоянное поперечное сечение, изготовленных из одного материала и при постоянной силе. Для бруса, имеющего несколько участков, отличающихся материалом, размерами сечения, продольной силой, изменение длины всего бруса определяется, как алгебраическая сумма удлинений или укорочений отдельных участков:

Описанный ранее опыт с резиновым брусом, на котором нанесена сетка линий, показал, что при растяжении поперечные размеры бруса уменьшаются, а при сжатии – увеличиваются, т. е. брус становится либо тоньше, либо толще. Это явление характерно для брусьев, изготовленных из всех материалов.
Опытным путем установлено, что при одноосном растяжении или сжатии отношение относительных поперечной и продольной деформаций для данного материала – величина постоянная.

Впервые на эту зависимость указал французский ученый С. Пуассон (1781-1840 г.г.) и математически она записывается так:

где ν – коэффициент поперечной деформации, называемый коэффициентом Пуассона .

Коэффициент Пуассона является безразмерной величиной, и характеризует упругие свойства материала. При растяжении и сжатии этот коэффициент принимается одинаковым.
Значения коэффициента Пуассона для разных материалов установлены опытным путем и их величины можно найти в соответствующих справочниках.

При статическом (медленном) растяжении образца растягивающая сила F возрастает от нуля до какого-то значения, удлиняет образец на величину Δl и при этом совершает работу W .
Эта работа аккумулируется в деформируемом образце в виде потенциальной энергии деформации U , причем, пренебрегая незначительными потерями энергии (например, тепловыми), можно считать, что W = U .

Путем изучения диаграмм растяжения образцов, установлено, что потенциальная энергия упругой деформации стержня длиной l постоянного поперечного сечения А при одинаковой во всех сечениях продольной силе N = F будет равна:

U = W = F Δl / 2 = N 2 l / (2E А)

Сопротивление материалов оперирует, также, таким понятием, как удельная потенциальная энергия деформации , которая подсчитывается, как потенциальная энергия, приходящаяся на единицу объема бруса.

При одновременном действии растягивающих и сжимающих нагрузок или ступенчатом изменении размеров поперечного сечения бруса, его разбивают на однородные участки и для каждого подсчитывают потенциальную энергию деформации. Потенциальную энергию деформации всего бруса определяют, как сумму потенциальных энергий отдельных участков.

Анализируя формулу потенциальной энергии деформации можно сделать вывод, что эта величина всегда положительная, поскольку в ее выражения входят квадраты линейных и силовых величин. По этой причине при вычислении потенциальной энергии деформации нельзя применять принцип независимости действия сил (поскольку квадрат суммы не равен сумме квадратов слагаемых).
Единицей измерения потенциальной энергии деформации, как и работы, является джоуль (Дж) .

Материалы раздела "Растяжение и сжатие":

Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.

1. Задачи сопротивления материалов
2. Классификация сил
3. Понятие о деформациях и напряжениях
4. Вычисление напряжений по площадкам, перпендикулярным к оси стержня
5. Деформации при растяжении и сжатии. Закон Гука. Коэффициент поперечной деформации
6. Механические характеристики свойств материала
7. Статически неопределимые задачи при растяжении и сжатии
8. Напряжения, возникающие при изменении температуры
9. Напряжения по наклонным сечениям при осевом растяжении и сжатии (линейное напряженное состояние)
10. Понятие о главных напряжениях. Виды напряженного состояния материалов
11. Плосконапряженное состояние материалов
12. Графическое определение напряжений (круг Мора)
13. Объемно-напряженное состояние материала
14. Деформации при плоском и объемном напряженных состояниях (обобщенный закон Гука)
15. Потенциальная энергия при сложном напряженном состоянии
16. Проверка прочности материала при сложном напряженном состоянии
17. Понятие о сдвиге. Расчет заклепок на перерезывание
18. Проверка заклепок на смятие и листов на разрыв
19. Расчет сварных соединений
20. Чистый сдвиг. Определение главных напряжений
21. Связь между напряжениями и деформацией при чистом сдвиге. Потенциальная энергия сдвига

Приведённый ознакомительный фрагмент книги Сопротивление материалов. Шпаргалка для студентов (Р. Н. Сиренко, 2009) предоставлен нашим книжным партнёром — компанией ЛитРес.

5. Деформации при растяжении и сжатии. Закон Гука. Коэффициент поперечной деформации

Некоторые элементы конструкций и элементов подвергаются только продольным нагрузкам, что вызывает в них деформацию растяжения или сжатия. Длина стержня, подвергнутого растяжению, увеличивается, а площадь его поперечного сечения уменьшается. При сжатии наоборот – длина уменьшается, а площадь сечения увеличивается. При этом изменение длины называют линейной продольной деформацией, а изменение площади поперечного сечения – поперечной линейной деформацией. Для оценки интенсивности деформации применяют такие понятия, как относительная продольная ε и относительная поперечная ε' – деформации, приходящиеся на единицу длины или пощади сечения стержня.

где Δl – изменение длины стержня;

Δa – изменение площади сечения.

Продольную деформацию растяжения обычно считают положительной, деформацию сжатия – отрицательной. Продольная и поперечная деформации связаны соотношением

μ – коэффициент поперечной деформации, который имеет свое значение для разных тел (в пределах упругого деформирования). Этот коэффициент называют коэффициентом Пуассона.

В пределах упругого деформирования экспериментально была установлена прямая зависимость между нормальным напряжением σ и относительной деформацией ε.

σ = Eε

Это соотношение носит название закона Гука, а коэффициент пропорциональности E называется модулем упругости первого рода. Модуль упругости – это величина, постоянная для каждого материала. Из соотношения видно, что при постоянном напряжении деформация меньше при большем модуле упругости.

Если рассматривать участок длиной l, на котором продольная сила и площадь поперечного сечения постоянны, закон Гука можно представить в виде:

Произведение EA называется жесткостью сечения.

При растяжении или сжатии стержня его сечения перемещаются. Осевое перемещение сечений друг относительно друга равно изменению длины стержня между этими сечениями. График, на котором изображены перемещения всех сечений относительно одного, принятого за неподвижное, называется эпюром перемещений.

Иметь представление о продольных и поперечных деформациях и их связи.

Знать закон Гука, зависимости и формулы для расчета напряжений и перемещений.

Уметь проводить расчеты на прочность и жесткость статически определимых брусьев при растяжении и сжатии.

Деформации при растяжении и сжатии

Рассмотрим деформацию бруса под действием продольной силы F (рис. 21.1).

В сопротивлении материалов принято рассчитывать деформации в относительных единицах:

Между продольной и поперечной деформациями существует зависимость

где μ— коэффициент поперечной деформации, или коэффициент Пуассона, —характеристика пластичности материала.

Закон Гука

В пределах упругих деформаций деформации прямо пропорциональны нагрузке:

где F — действующая нагрузка; к — коэффициент. В современной форме:

где Е — модуль упругости, характеризует жесткость материала.

В пределах упругости нормальные напряжения пропорциональны относительному удлинению.

Значение Е для сталей в пределах (2 – 2,1) • 10 5 МПа. При прочих равных условиях, чем жестче материал, тем меньше он деформируется:

Формулы для расчета перемещений поперечных сечений бруса при растяжении и сжатии

Используем известные формулы.

В результате получим зависимость между нагрузкой, размерами бруса и возникающей деформацией:

Δl — абсолютное удлинение, мм;

σ — нормальное напряжение, МПа;

l — начальная длина, мм;

Е — модуль упругости материала, МПа;

N — продольная сила, Н;

А — площадь поперечного сечения, мм 2 ;

Произведение АЕ называют жесткостью сечения.

Выводы

1. Абсолютное удлинение бруса прямо пропорционально величине продольной силы в сечении, длине бруса и обратно пропорционально площади поперечного сечения и модулю упругости.

2. Связь между продольной и поперечной деформациями зависит от свойств материала, связь определяется коэффициентом Пуассона, называемом коэффициентом поперечной деформации.

Коэффициент Пуассона: у стали μ от 0,25 до 0,3; у пробки μ = 0; у резины μ = 0,5.

3. Поперечные деформации меньше продольных и редко влияют на работоспособность детали; при необходимости поперечная деформация рассчитывается через продольную.

где Δа — поперечное сужение, мм;

а_о — начальный поперечный размер, мм.

4.
Закон Гука выполняется в зоне упругих деформаций, которая определяется при испытаниях на растяжение по диаграмме растяжения (рис. 21.2).

При работе пластические деформации не должны возникать, упругие деформации малы по сравнению с геометрическими размерами тела. Основные расчеты в сопротивлении материалов проводятся в зоне упругих деформаций, где действует закон Гука.

На диаграмме (рис. 21.2) закон Гука действует от точки 0 до точки 1.

5. Определение деформации бруса под нагрузкой и сравнение ее с допускаемой (не нарушающей работоспособности бруса) называют расчетом на жесткость.

Примеры решения задач

Пример 1. Дана схема нагружения и размеры бруса до деформации (рис. 21.3). Брус защемлен, определить перемещение свободного конца.

Решение

1.
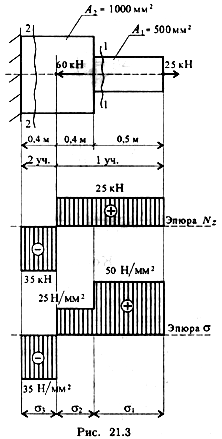
Брус ступенчатый, поэтому следует построить эпюры продольных сил и нормальных напряжений.

Делим брус на участки нагружения, определяем продольные силы, строим эпюру продольных сил.

2. Определяем величины нормальных напряжений по сечениям с учетом изменений площади поперечного сечения.

Строим эпюру нормальных напряжений.

3. На каждом участке определяем абсолютное удлинение. Результаты алгебраически суммируем.

Примечание. Балка защемлена, в заделке возникает неизвестная реакция в опоре, поэтому расчет начинаем со свободного конца (справа).

1. Два участка нагружения:

Три участка по напряжениям:

Пример 2. Для заданного ступенчатого бруса (рис. 2.9, а) построить эпюры продольных сил и нормальных напряжений по его длине, а также определить перемещения свободного конца и сечения С, где приложена сила Р₂. Модуль продольной упругости материала Е = 2,1 • 10 5 Н/'мм 3 .

Решение

1. Заданный брус имеет пять участков /, //, III, IV, V (рис. 2.9, а). Эпюра продольных сил показана на рис. 2.9, б.

2. Вычислим напряжения в поперечных сечениях каждого участка:

Эпюра нормальных напряжений построена на рис. 2.9, в.

3. Перейдем к определению перемещений поперечных сечений. Перемещение свободного конца бруса определяется как алгебраическая сумма удлинений (укорочений) всех его участков:

Подставляя числовые значения, получаем

4. Перемещение сечения С, в котором приложена сила Р₂, определяется как алгебраическая сумма удлинений (укорочений) участков ///, IV, V:

Подставляя значения из предыдущего расчета, получаем

Таким образом, свободный правый конец бруса перемещается вправо, а сечение, где приложена сила Р₂, — влево.

5. Вычисленные выше значения перемещений можно получить и другим путем, пользуясь принципом независимости действия сил, т. е. определяя перемещения от действия каждой из сил Р₁; Р_2; Р₃ в отдельности и суммируя результаты. Рекомендуем учащемуся проделать это самостоятельно.

Пример 3. Определить, какое напряжение возникает в стальном стержне длиной l = 200 мм, если после приложения к нему растягивающих сил его длина стала l₁ = 200,2 мм. Е = 2,1*10 6 Н/мм 2 .

Решение

Абсолютное удлинение стержня

Продольная деформация стержня

Согласно закону Гука

Пример 4. Стенной кронштейн (рис. 2.10, а) состоит из стальной тяги АВ и деревянного подкоса ВС. Площадь поперечного сечения тяги F₁ = 1 см 2 , площадь сечения подкоса F₂ = 25 см 2 . Определить горизонтальное и вертикальное перемещения точки В, если в ней подвешен груз Q = 20 кН. Модули продольной упругости стали E_ст = 2,1*10 5 Н/мм 2 , дерева Е_д = 1,0*10 4 Н/мм 2 .

Решение

1. Для определения продольных усилий в стержнях АВ и ВС вырезаем узел В. Предполагая, что стержни АВ и ВС растянуты, направляем возникающие в них усилия N₁ и N₂ от узла (рис. 2.10, 6). Составляем уравнения равновесия:

Усилие N₂ получилось со знаком минус. Это указывает на то, что первоначальное предположение о направлении усилия неверно — фактически этот стержень сжат.

2. Вычислим удлинение стальной тяги Δl₁ и укорочение подкоса Δl₂:

Тяга АВ удлиняется на Δl₁ = 2,2 мм; подкос ВС укорачивается на Δl₁ = 7,4 мм.

3. Для определения перемещения точки В мысленно разъединим стержни в этом шарнире и отметим их новые длины. Новое положение точки В определится, если деформированные стержни АВ₁ и В₂С свести вместе путем их вращения вокруг точек А и С (рис. 2.10, в). Точки В₁ и В₂ при этом будут перемещаться по дугам, которые вследствие их малости могут быть заменены отрезками прямых В₁В' и В₂В', соответственно перпендикулярными к АВ₁ и СВ₂. Пересечение этих перпендикуляров (точка В') дает новое положение точки (шарнира) В.

4. На рис. 2.10, г диаграмма перемещений точки В изображена в более крупном масштабе.

5. Горизонтальное перемещение точки В

где составляющие отрезки определяются из рис. 2.10, г;

Подставляя числовые значения, окончательно получаем

При вычислении перемещений в формулы подставляются абсолютные значения удлинений (укорочений) стержней.

Контрольные вопросы и задания

1. Стальной стержень длиной 1,5 м вытянулся под нагрузкой на 3 мм. Чему равно относительное удлинение? Чему равно относительное сужение? (μ = 0,25.)

2. Что характеризует коэффициент поперечной деформации?

3. Сформулируйте закон Гука в современной форме при растяжении и сжатии.

4. Что характеризует модуль упругости материала? Какова единица измерения модуля упругости?

5. Запишите формулы для определения удлинения бруса. Что характеризует произведение АЕ и как оно называется?

6. Как определяют абсолютное удлинение ступенчатого бруса, нагруженного несколькими силами?

7. Ответьте на вопросы тестового задания.

Основные понятия. Метод сечений.

Растяжение или сжатие возникает, когда равнодействующие внешних нагрузок действуют вдоль оси стержня. В поперечном сечении стержня имеет место только одна внутренняя сила N, действующая вдоль его оси. Эту внутреннюю силу называют продольной силой или нормальной силой (действует по нормали к поперечному сечению). На рис. 2.1 изображен прямой стержень, работающий на растяжение.

Рис 2.1. Прямой стержень, работающий на растяжение

Правило знаков для продольной силы. Продольная сила будет положительной, если она вызывает растяжение, т.е., направлена от сечения.

Рис 2.2. К правилу знака продольной силы N

Знак сжимающей силы имеет значение в расчетах на прочность в строительстве. Бетон, кирпичная или каменная кладка плохо работают на растяжение и хорошо – на сжатие. Например, арки древних каменных храмов, сохранившиеся до сегодняшних дней – это элементы строительных конструкций, в поперечных сечениях которых имеют место только сжимающие продольные силы. Конечно, древние строители не выполняли расчетов, а набирали опыт по мере работы.

Сталь одинаково хорошо сопротивляется и сжатию, и растяжению. Стальную арматуру закладывают в растянутые зоны бетона для того, чтобы он не разрушался от растяжения. Получившийся материал называется железобетоном.

Метод сечений. Для определения внутренних усилий в стержнях используется метод сечений, суть которого состоит в следующем.

1. Разрезают стержень на две части плоскостью, перпендикулярной оси (проводят поперечное сечение).

2. Отбрасывают одну из двух частей стержня.

3. Заменяют действие отброшенной части на оставшуюся часть стержня неизвестными внутренними усилиями.

4. Уравнения равновесия, составленные для оставшейся части стержня, позволяют определить внутренние усилия.

Дифференциальная зависимость между q и N

Рис 2.3. К выводу дифференциальной зависимости между q и N

Отсюда получаем дифференциальную зависимость между q и N:

Первая производная от продольной силы по переменной х равна с обратным знаком интенсивности продольной нагрузки. Исходя из свойств производной, из (2.1) можно сделать вывод о том, что, если q(x) является полиномом n степени, то N(x)будет представлять собой полином n+1степени. Это позволяет определить, какой вид будет иметь график функции N(x)в зависимости от q(х). В дальнейшем нам пригодятся для изучения курса три следствия:

1) если q = 0 (т. е. нагрузка q отсутствует), то N(x) = const;

2) если q(x) = const, то есть является равномерно распределенной нагрузкой, то N(x) – линейная функция;

3) если q(x) = линейная функция, то N(x) – квадратная парабола.

Эпюра продольных сил

Эпюрой продольных сил называется график функции N(x).

Рассмотрим прямой стержень, загруженный продольными нагрузками и находящийся в равновесии (рис. 2.4). Предположим, что ось Ох (на рисунке не показана), направлена вправо.

Рис 2.4. Определение продольной силы методом сечений

Определим продольную силу в произвольном сечении К.

В соответствии с методом сечений отбросим левую часть и составим уравнение равновесия для правой части, направив неизвестную силу N от сечения (предполагая ее растягивающей):

Находим продольную силу:

Таким образом, продольную силу в поперечном сечении можно найти суммированием внешних сил, которые находятся справа от сечения.

Отбросим теперь правую часть и рассмотрим уравнение равновесия для левой части:

Находим продольную силу:

Отсюда следует, что продольную силу в поперечном сечении можно найти также суммированием внешних сил, которые находятся слева от сечения.

На основании формул (2.2) и (2.3) можно сделать следующий вывод: продольная сила в поперечном сечении стержня – это сумма проекций на ось стержня внешних сил, расположенных по одну сторону от сечения.

Продольной силой можно считать проекцию главного вектора системы внешних сил, расположенных с одной стороны от сечения, на ось стержня. Эта проекция приложена в точке центра тяжести сечения, причем, если она направлена в сторону внешней нормали по отношению к оставшейся части, то она будет положительной.

Проиллюстрируем, как можно найти силу N в произвольном сечении (рис. 2.5).

Рис 2.5. К определению продольной силы

Отметим некоторые общие правила построения эпюр продольных сил.

Эпюра строится на линии, параллельной оси стержня (иногда ее называют базовой линией или базой эпюры). Через характерные сечения проводятся выносные линии, на которых в определенном масштабе откладываются значения N в этих сечениях и соединяются линиями. Над эпюрой указывается обозначение функции (в данных примерах N) и ее размерность. Эпюра заштриховывается перпендикулярно оси, при этом каждая штриховая линия как бы указывает значение N в соответствующем сечении. Внутри эпюры в кружочках указывается знак N на соответствующем участке. При этом, как правило, положительные значения откладываются в правую сторону (если эпюра построена на горизонтальной линии, то положительные значения откладывают вверх).

На основании изучения построенных эпюр и следствий из дифференциальной зависимости можно отметить характерные особенности эпюры N, которые обычно используют для ее контроля.

1. В сечении, где приложена сосредоточенная сила, на эпюре N имеется скачок на величину этой силы.

2. На участке, где приложена равномерно распределенная нагрузка, эпюра N имеет линейный характер, причем изменение функции N(х) на участке равно ql.

3. На участке, где отсутствует распределенная нагрузка, эпюра N является постоянной.

Напряжения и деформации. Закон Гука

Нормальные напряжения в поперечных сечениях. При центральном растяжении (сжатии) стержней в их поперечных сечениях действует только одно внутреннее усилие – продольная сила N.

В соответствии с гипотезой плоских сечений сечения, плоские и перпендикулярные оси стержня до деформации, остаются плоскими и перпендикулярными оси после деформации.

Можно показать, что применение этой гипотезы приводит к простой формуле для определения нормальных напряжений при растяжении и сжатии.

Эти напряжения постоянны по сечению (рис. 2.5)

Рис 2.5. Распределение нормальных напряжений по сечению при растяжении

Напряжения на наклонных площадках. Рассмотрим элемент стержня, образованный поперечным и наклонным к оси стержня сечениями (рис. 2.7, а). Стержень растягивается силами F по его концам.

Рис 2.7. Напряжения на наклонных площадках

Обозначим площадь наклонного сечения А, тогда площадь горизонтальной площадки будет равна А ×соs α (рис. 2.7,б), где α – угол поворота нормали наклонного сечения относительно оси х. Очевидно, что продольная сила равна N = F = s_х × (А соs α) = p_n А и постоянна по длине стержня. Поэтому полные напряжения p_n = s_х соs α.

Обозначая s_x = s, из этих уравнений найдем

Из равенств (2.7) видно, что s_a и t_a являются периодическими функциями, зависящими от угла a наклона сечения. При различных углах a:

а) a = 0 (поперечное сечение); s_a = s; t_a = 0;

б) a = 90° (продольное сечение); s_a = 0; t_a = 0;

в) a = 45° (наклонное под углом 45° сечение); s_a = s /2; t_a = s/2.

Максимальные нормальные напряжения возникают в поперечных сечениях и определяются по формуле (2.5).

Деформации. Рассмотрим деформированное состояние стержней при растяжении и сжатии. При растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии – наоборот. Это легко наблюдать в опытах с резиновыми образцами, в которых деформации достаточно велики.

Рис 2.8. Деформирование стержня при растяжении

Рассмотрим, какие деформации возникают при растяжении стержня (рис. 2.8).

Величина Dl = l – l₀ называется абсолютным удлинением, или абсолютной линейной продольной деформацией стержня(здесь l₀ – первоначальная длина, а l – длина после деформации). Величины Dh = h – h₀ и Db= b – b₀ называются абсолютными линейными поперечными деформациями (здесь h₀ и b₀ – первоначальные поперечные размеры, h и b – поперечные размеры после деформации). Абсолютные деформации измеряются в единицах длины (метрах, сантиметрах, миллиметрах).

Учитывая, что продольные и поперечные деформации имеют разный знак, будет справедливым следующее выражение:

Обозначая e_x = e, e_y = e_z = e¢, формулу для определения коэффициента Пуассона можно переписать в часто встречающемся в учебниках по сопротивлению материалов виде:

Закон Гука. Связь между напряжениями и деформациями была установлена экспериментально в 1676 г. английским ученым Робертом Гуком Эта связь в случае одноосного растяжения (сжатия) имеет вид

и называется законом Гука. Для краткости можно опустить индексы и записать закон Гука в виде

Коэффициент пропорциональности Е, входящий в закон Гука, называется модулем упругости, или модулем Юнга. Модуль упругости является второй упругой характеристикой материалов после коэффициента Пуассона и характеризует важное их свойство – жесткость. Чем больше Е, тем более жесткий материал мы имеем.

Учитывая, что линейные деформации являются безразмерными величинами, можно заключить, что размерность модуля упругости такая же, как и у напряжений (МПа).

Рис 2.9. Графическое изображение закона Гука

Значения модуля Юнга для разных материалов лежат в очень широких пределах. Например, для резины он равен 1–10 МПа, а для стали – больше 2·10 5 МПа. В табл. 2.1 приведены примерные значения Е для некоторых материалов.

Модули упругости Е и коэффициенты Пуассона ν

(примерные величины)

Дата добавления: 2018-10-27 ; просмотров: 298 ;

Читайте также: